Ein Tutorial zu Streudiagrammen: Eine schnelle Anleitung

Einführung

Im Bereich der Datenanalyse und -visualisierung dienen Streudiagramme als unverzichtbare Werkzeuge, um Beziehungen zwischen Variablen aufzudecken. In unserem speziellen Fall haben wir ein Streudiagramm erstellt, das die faszinierende Verbindung zwischen Arm- und Körpergröße bei einer Gruppe von Schülerinnen und Schülern der 11. Klasse untersucht. Diese visuelle Darstellung der Daten, bestehend aus acht einzelnen Datenpunkten, ermöglicht es uns, die Dynamik zwischen diesen beiden Merkmalen zu erforschen. Durch die Analyse der Muster im Streudiagramm können wir beginnen, Vorhersagen über die Arm- oder Körpergröße basierend auf der jeweils anderen Größe zu treffen. Diese Analyse beleuchtet nicht nur die körperlichen Merkmale dieser Schüler, sondern zeigt auch die Stärke von Streudiagrammen auf, Korrelationen aufzudecken.

Was ist ein Streudiagramm

Ein Streudiagramm, auch bekannt als Streudiagramm oder Streuplot, ist eine Art der Datenvisualisierung, die verwendet wird, um die Beziehung zwischen zwei Variablen darzustellen. Jeder Punkt auf dem Diagramm repräsentiert einen einzelnen Datenpunkt, und die Position des Punktes wird durch die Werte der beiden Variablen bestimmt. Streudiagramme sind nützlich, um Muster, Trends und Korrelationen in Daten zu erkennen. Im Folgenden werde ich eine umfassende Erklärung von Streudiagrammen geben und Beispiele anführen, um ihre Anwendung zu veranschaulichen.

Bestandteile eines Streudiagramms:

1. X-Achse: Die horizontale Achse stellt eine der analysierten Variablen dar.
2. Y-Achse: Die vertikale Achse stellt die andere analysierte Variable dar.
3. Datenpunkte: Jeder Datenpunkt auf dem Diagramm repräsentiert eine einzelne Beobachtung oder Datengruppe, wobei ein Wert für die X-Achsen-Variable und ein weiterer Wert für die Y-Achsen-Variable angegeben wird.
4. Titel: Ein Titel am oberen Rand des Diagramms gibt Kontext und Informationen darüber, was das Diagramm darstellt.
5. Achsenbeschriftungen: Beschriftungen auf der X- und Y-Achse geben Informationen über die Einheiten oder Kategorien der Variablen an.
6. Legende: Wenn mehrere Datensätze auf demselben Diagramm dargestellt werden, kann eine Legende verwendet werden, um sie zu unterscheiden.

Beispiele für Streudiagramme:

1. Starke positive Korrelation:
   • Definition: Der Wert von Y steigt, wenn der Wert von X steigt.
   • Beispiel: In einer Studie über die Anzahl der Studienstunden und die Prüfungsnoten steigen die Prüfungsnoten (Y) ebenfalls, wenn die Anzahl der Studienstunden (X) zunimmt. Dies zeigt eine starke positive Korrelation an.
2. Starke negative Korrelation:
   • Definition: Der Wert von Y sinkt, wenn der Wert von X steigt.
   • Beispiel:In einer Studie zur Niederschlagsmenge und der Anzahl der Stunden, die Menschen im Freien verbringen, nimmt die Anzahl der Stunden im Freien (Y) ab, wenn die Niederschlagsmenge (X) zunimmt. Dies zeigt eine starke negative Korrelation.
3. Schwache positive Korrelation:
   • Definition:Der Wert von Y steigt leicht, wenn der Wert von X steigt.
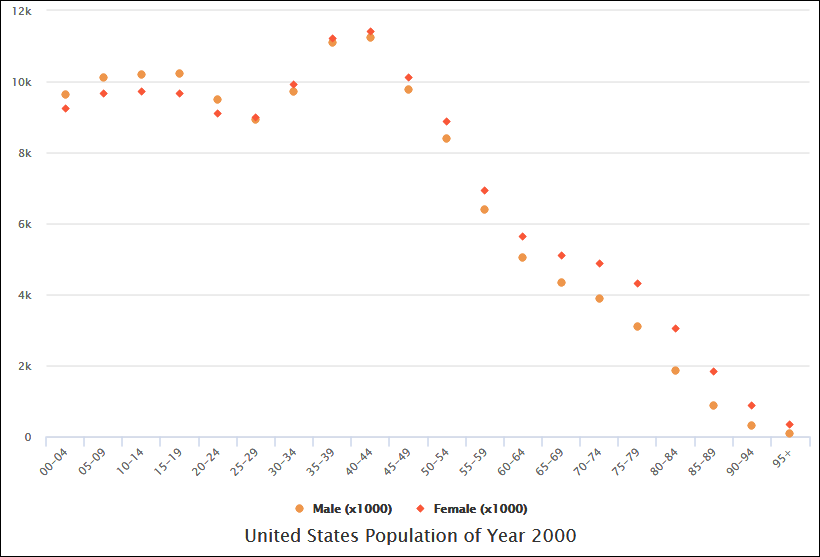
   • Beispiel:Bei der Analyse des Alters von Personen und ihres jährlichen Einkommens könnte man feststellen, dass das Einkommen (Y) leicht steigt, wenn das Alter (X) zunimmt. Dies deutet auf eine schwache positive Korrelation hin.
4. Schwache negative Korrelation:
   • Definition:Der Wert von Y sinkt leicht, wenn der Wert von X steigt.
   • Beispiel:Bei der Untersuchung der Zeit, die für die Pendelzeit zur Arbeit aufgewendet wird, und der Energielevel könnte man feststellen, dass die Energielevel (Y) leicht sinken, wenn die Pendelzeit (X) leicht zunimmt. Dies deutet auf eine schwache negative Korrelation hin.
5. Komplexe Korrelation:
   • Definition:Der Wert von Y scheint mit dem Wert von X verbunden zu sein, aber die Beziehung ist nicht leicht zu bestimmen.
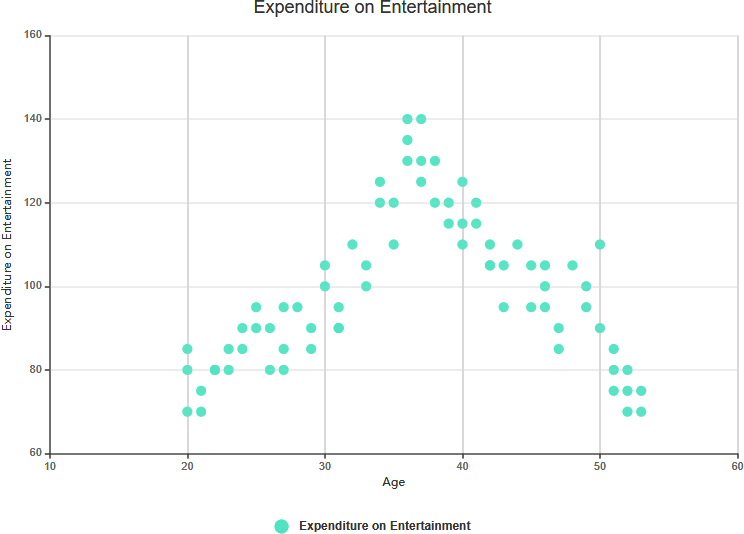
   • Beispiel:Bei der Analyse der Werbeausgaben und des Produktumsatzes könnte die Beziehung zwischen beiden komplex erscheinen, mit Schwankungen und keiner klaren Richtung.
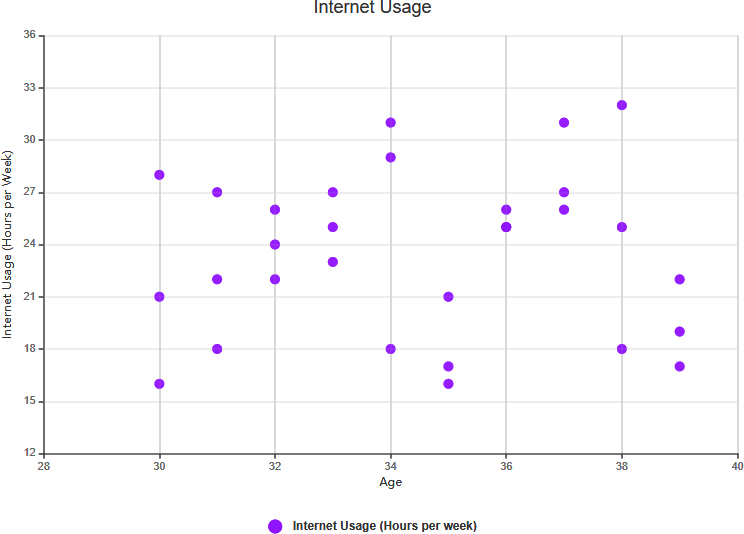
6. Keine Korrelation:
   • Definition:Es besteht kein nachweisbarer Zusammenhang zwischen den beiden Variablen.
   • Beispiel:Wenn Sie die Schuhgröße und IQ-Werte untersuchen, könnten Sie feststellen, dass zwischen ihnen kein signifikanter Zusammenhang besteht. In diesem Fall besteht keine Korrelation.

Das Verständnis dieser Korrelationsmuster ist entscheidend für die Interpretation von Streudiagrammen und die Ableitung sinnvoller Schlussfolgerungen aus Daten. Die Korrelationsanalyse hilft bei der Vorhersage, dem Verständnis von Ursache-Wirkungs-Beziehungen und der Identifizierung von Trends in verschiedenen Bereichen wie Wirtschaft, Sozialwissenschaften und Naturwissenschaften.

Starke positive Korrelation

Dieses Diagramm bearbeiten

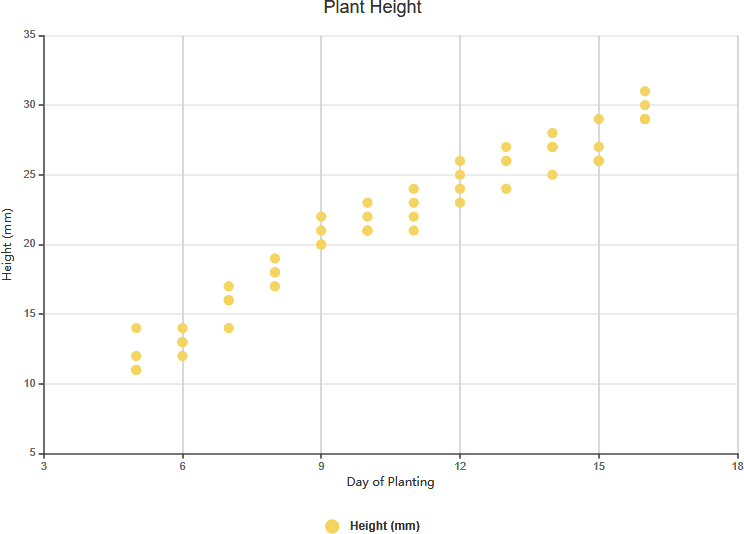
Starke negative Korrelation

Dieses Diagramm bearbeiten

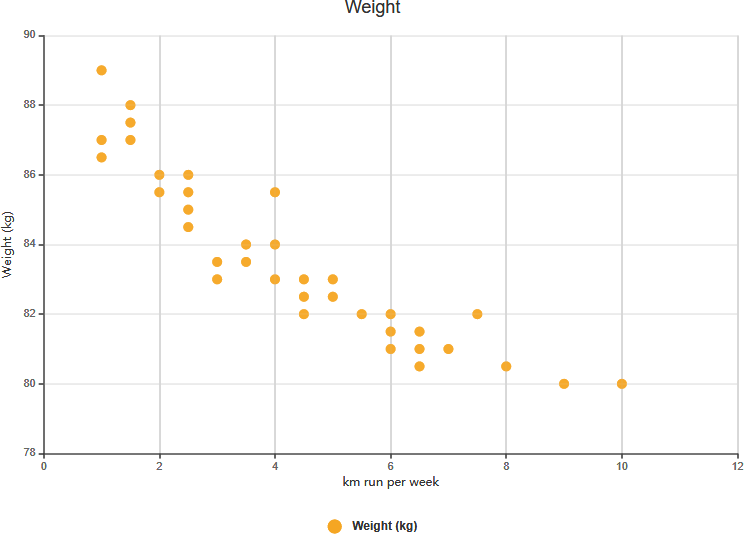
Schwache positive Korrelation

Dieses Diagramm bearbeiten

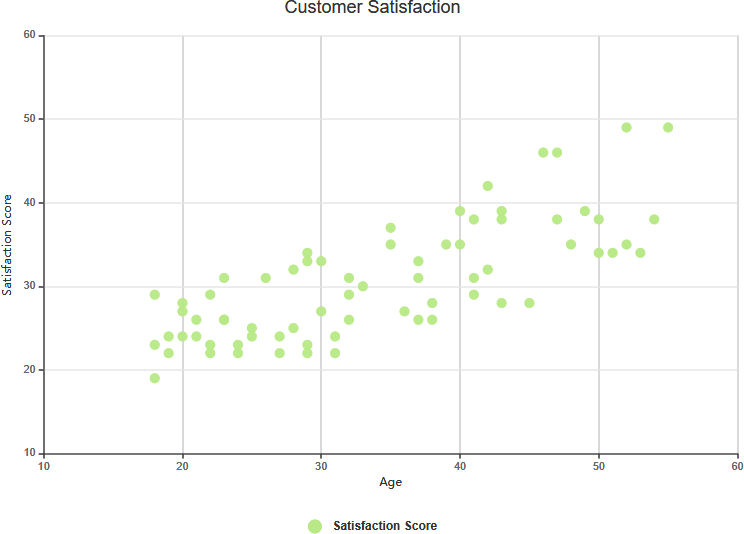
Komplexe Korrelation

Dieses Diagramm bearbeiten

Keine Korrelation

Dieses Diagramm bearbeiten

Beispiel für ein Streudiagramm: Arm-Länge im Vergleich zu Klasse 11

Das oben gezeigte Streudiagramm veranschaulicht Daten zur Körpergröße und Arm-Länge von acht Schülerinnen und Schülern der Klasse 11. Durch die Analyse der Beziehung zwischen der Körpergröße und der Arm-Länge eines Schülers können wir einen Trend erkennen. Dieser Trend ermöglicht es uns, die Arm-Länge eines Schülers anhand seiner Körpergröße abzuschätzen und umgekehrt. In diesem speziellen Diagramm ist eine positive Korrelation zwischen Arm-Länge und Körpergröße deutlich erkennbar.

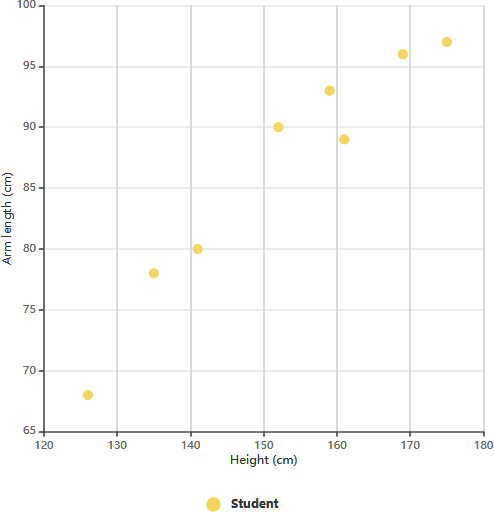
Nachdem die Korrelation zwischen diesen Variablen festgestellt wurde, können wir Vorhersagen über das Verhalten der abhängigen Variable anhand der Messwerte der unabhängigen Variable treffen. Dieses Diagramm erweist sich als besonders wertvoll, wenn eine der Variablen leicht messbar ist, während die andere nicht leicht zugänglich ist. Zum Beispiel können wir bei einem Schüler der Klasse 11 mit einer Körpergröße von 148 cm schätzen, dass seine Arm-Länge etwa 84 cm beträgt.

Fazit

In diesem Streudiagramm haben wir die Grundlagen von Streudiagrammen und ihre entscheidende Rolle bei der Datenvisualisierung und -analyse untersucht. Streudiagramme bieten eine leistungsfähige Möglichkeit, Beziehungen zwischen Variablen darzustellen und Muster in Daten aufzudecken. Lassen Sie uns einige zentrale Erkenntnisse aus diesem Tutorial zusammenfassen:

1. Streudiagramme definiert:Streudiagramme, auch bekannt als Streudiagramme oder Streupunktdiagramme, zeigen Datenpunkte in einer zweidimensionalen Ebene, wobei jeder Punkt eine eindeutige Beobachtung oder Datengruppe darstellt.
2. Variablen und Achsen:Streudiagramme bestehen typischerweise aus zwei Achsen: der X-Achse und der Y-Achse. Diese Achsen repräsentieren die untersuchten Variablen und ermöglichen es, zu visualisieren, wie Veränderungen einer Variablen mit Veränderungen der anderen verbunden sind.
3. Korrelationsmuster:Streudiagramme helfen uns, verschiedene Korrelationsmuster zwischen Variablen zu erkennen. Diese Muster können als starke positive Korrelation, starke negative Korrelation, schwache positive Korrelation, schwache negative Korrelation, komplexe Korrelation oder keine Korrelation klassifiziert werden.
4. Beispiele aus der Praxis:Im Verlauf des Tutorials haben wir praktische Beispiele bereitgestellt, um jedes dieser Korrelationsmuster zu veranschaulichen. Von der Untersuchung der Körpergröße und Arm-Länge von Schülern bis hin zur Analyse der Beziehung zwischen Lernstunden und Prüfungsergebnissen haben wir gesehen, wie Streudiagramme in verschiedenen Bereichen eingesetzt werden können.
5. Vorhersagekraft:Streudiagramme ermöglichen es uns, Vorhersagen über eine Variable auf Basis der anderen zu treffen und liefern wertvolle Erkenntnisse für Entscheidungsfindung und das Verständnis kausaler Zusammenhänge.
6. Komplexe Daten:Streudiagramme sind vielseitige Werkzeuge, die komplexe Daten verarbeiten können, einschließlich Situationen, in denen die Beziehung zwischen den Variablen nicht eindeutig ist.
7. Dateninterpretation:Die Fähigkeit, Streudiagramme zu interpretieren, ist entscheidend für Forscher, Analysten und alle, die aus Daten sinnvolle Schlussfolgerungen ziehen möchten.
8. Praktische Anwendungen:Streudiagramme finden Anwendung in sehr unterschiedlichen Bereichen wie Wirtschaft, Sozialwissenschaften, Naturwissenschaften, Ingenieurwesen und vielen anderen. Sie helfen dabei, Trends, Korrelationen und Ausreißer innerhalb von Datensätzen zu identifizieren.

Durch die Beherrschung der Kunst, Streudiagramme zu erstellen, zu analysieren und zu interpretieren, erwerben Sie eine wertvolle Fähigkeit für datengestützte Entscheidungsfindung. Unabhängig davon, ob Sie Student, Forscher oder Fachkraft sind, sind Streudiagramme ein wertvolles Werkzeug in Ihrem Datenanalysetoolkit und liefern Erkenntnisse, die fundierte Entscheidungen und ein tieferes Verständnis in Ihrem Fachgebiet fördern.