de_DEen_USes_ESfa_IRfr_FRid_IDjapl_PLpt_PTru_RUvizh_CNzh_TW

散点图教程：快速指南

Table of Contents hide
1 引言
2 什么是散点图
3 散点图示例：臂长与11年级
4 结论

引言

在数据分析与可视化领域，散点图是揭示变量之间关系的宝贵工具。在本例中，我们生成了一个散点图，用于探索一组11年级学生臂长与身高之间的有趣关联。这一由八个独立数据点组成的可视化数据表示，使我们能够深入探讨这两个属性之间的动态关系。通过研究散点图中的模式，我们可以开始根据身高预测臂长，或根据臂长预测身高。这项分析不仅揭示了这些学生的身体特征，也展示了散点图在揭示相关性方面的强大作用。

Scatter chart example

什么是散点图

一种散点图，也称为散点图或散点图，是一种用于展示两个变量之间关系的数据可视化类型。图表中的每个点代表一个单独的数据点，该点的位置由两个变量的值决定。散点图有助于识别数据中的模式、趋势和相关性。下面，我将提供对散点图的全面解释，并通过示例说明其应用。

散点图的组成部分：

  1. X轴： 横轴代表被分析的其中一个变量。
  2. Y轴： 纵轴代表被分析的另一个变量。
  3. 数据点： 图表中的每个数据点代表一次观测或一个数据对，分别对应X轴变量和Y轴变量的一个值。
  4. 标题： 图表顶部的标题提供上下文信息，说明图表所代表的内容。
  5. 坐标轴标签： X轴和Y轴上的标签提供有关变量单位或类别的信息。
  6. 图例： 如果在同一张图表上显示多个数据集，可以使用图例来区分它们。

散点图示例：

散点图呈现出多种相关性模式，每种模式都反映了X值与Y值之间的关联。为了说明这些模式，我们为每种情况提供示例：

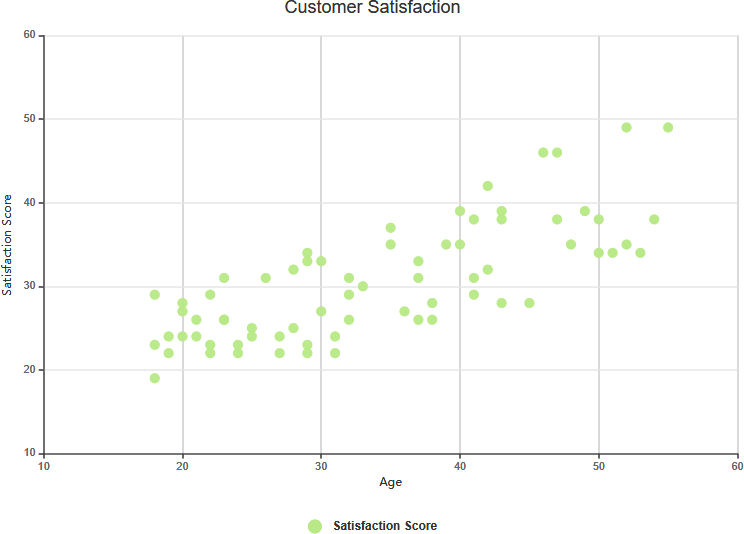
  1. 强正相关：
    • 定义： 当X的值增加时，Y的值也随之增加。
    • 示例： 在一项关于学习时间与考试成绩的研究中，随着学习时间（X）的增加，考试成绩（Y）也相应提高。这表明存在强正相关关系。
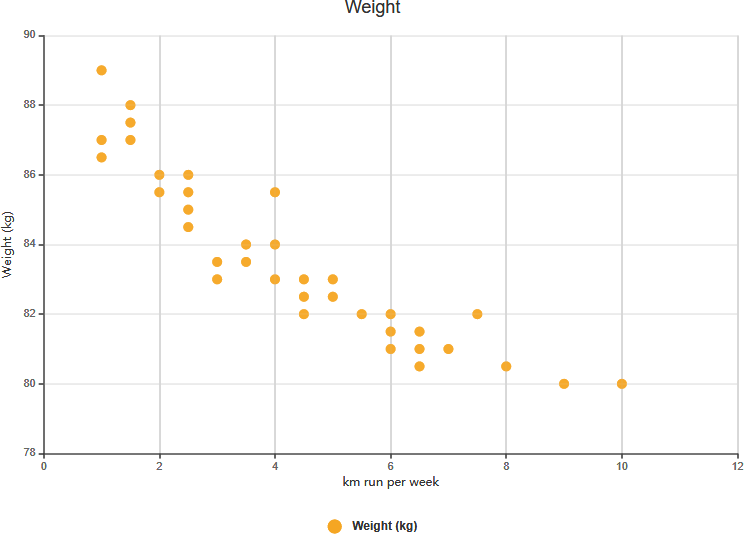
  2. 强负相关：
    • 定义： 当X的值增加时，Y的值减少。
    • 示例：在一项关于降雨量和人们户外停留时间的研究中，随着降雨量（X）的增加，户外停留时间（Y）减少。这表明存在强烈的负相关。
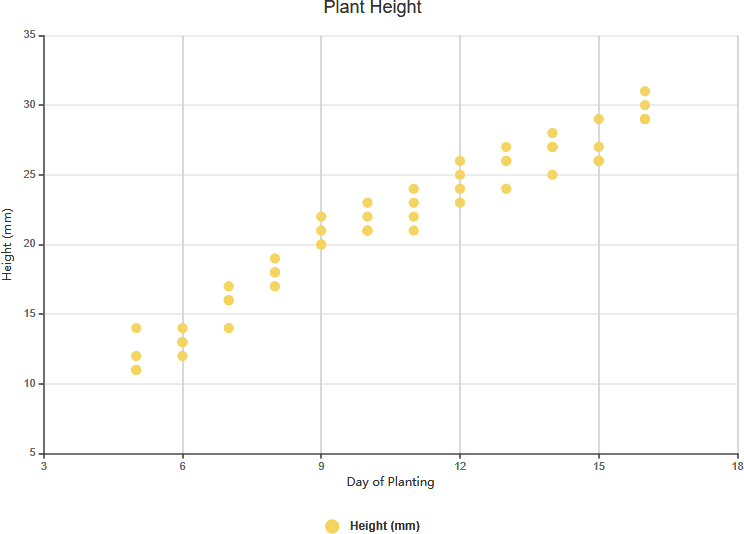
  3. 弱正相关：
    • 定义：随着X值的增加，Y值略有增加。
    • 示例：分析个人年龄与年收入，你可能会发现随着年龄（X）增加，收入（Y）略有上升。这表明存在弱正相关。
  4. 弱负相关：
    • 定义：随着X值的增加，Y值略有下降。
    • 示例：研究通勤时间与精力水平，你可能会注意到随着通勤时间（X）略有增加，精力水平（Y）略有下降。这表明存在弱负相关。
  5. 复杂相关：
    • 定义：Y的值似乎与X的值有关，但这种关系不易确定。
    • 示例：在分析广告支出与产品销量的关系时，两者之间的关系可能显得复杂，存在波动且无明确方向。
  6. 无相关性：
    • 定义：两个变量之间没有明显的关联。
    • 示例：如果你研究鞋码与智商分数，可能会发现两者之间没有显著关系。在这种情况下，两者无相关性。

理解这些相关性模式对于解读散点图并从数据中得出有意义的结论至关重要。相关性分析有助于预测、理解因果关系，并在经济学、社会科学和自然科学等多个领域识别趋势。

强正相关

Scatter chart example - Strong positive correlation

编辑此图表

强负相关

Scatter chart example - Strong negative correlation

编辑此图表

弱正相关

Scatter chart example - Weak positive correlation

编辑此图表

复杂相关

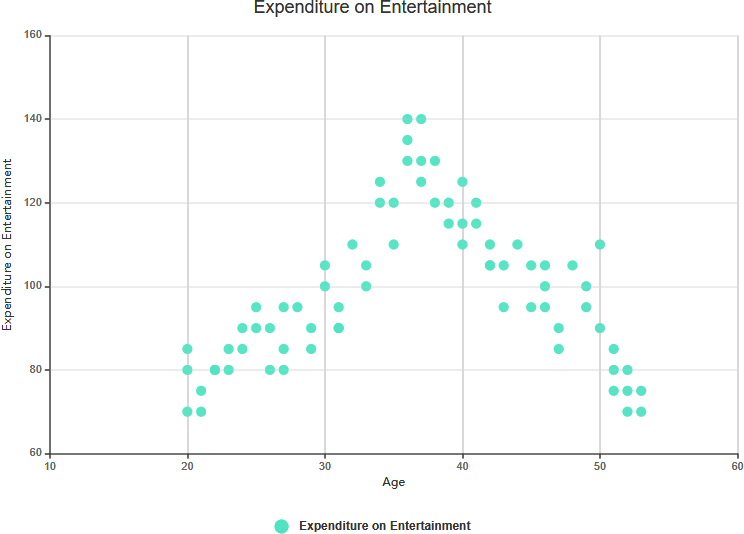
Scatter chart example - Complex correlation

编辑此图表


无相关性

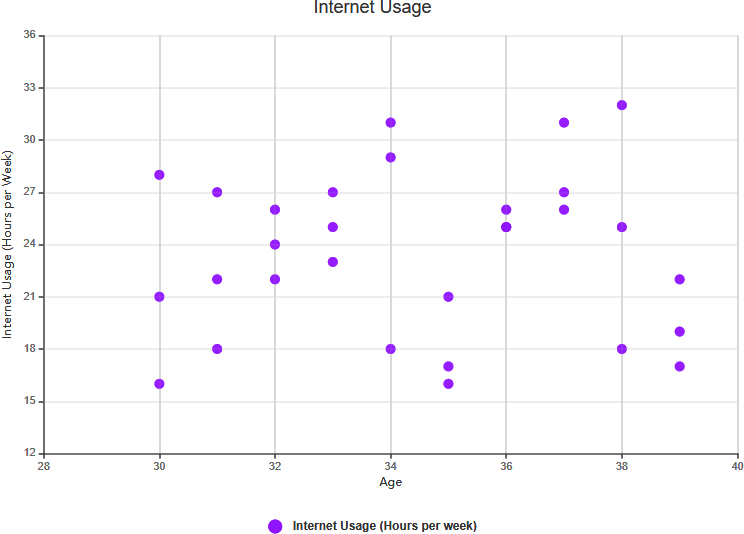
Scatter chart example - No correlation

编辑此图表

 

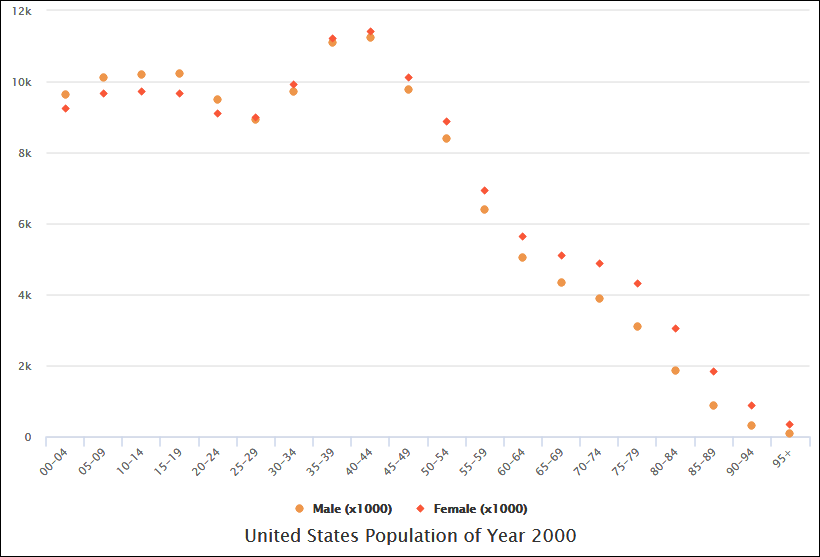
散点图示例：臂长与11年级

上图的散点图展示了八名11年级学生身高与臂长的数据。通过考察学生身高与臂长之间的关系，我们可以发现一种趋势。这一趋势使我们能够根据给定的身高估算学生的臂长，反之亦然。在此图表中，臂长与身高之间存在明显的正相关性。

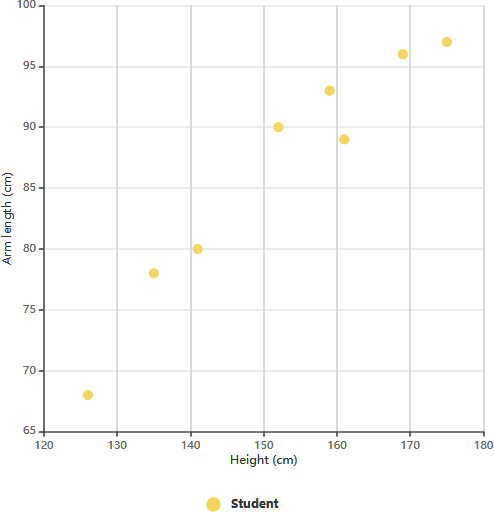
Scatter chart example - Arm length on guide 11

在确定这些变量之间的相关性后，我们可以利用自变量的测量值来预测因变量的行为。当其中一个变量容易测量而另一个不易测量时，此图表尤其有价值。例如，如果一名11年级学生的身高为148厘米，我们可以估算其臂长大约为84厘米。

结论

在本散点图中，我们探讨了散点图的基本原理及其在数据可视化与分析中的关键作用。散点图提供了一种强大的方式来展示变量之间的关系，并揭示数据中的模式。让我们回顾一下本教程中的几个关键要点：

  1. 散点图的定义：散点图，也称为散点图或散点图，将数据点显示在二维平面上，每个点代表一个独特的观测值或数据对。
  2. 变量与坐标轴：散点图通常由两个坐标轴组成：X轴和Y轴。这两个坐标轴代表研究中的变量，从而可以直观地展示一个变量的变化如何与另一个变量的变化相关联。
  3. 相关性模式：散点图帮助我们识别变量之间的不同相关性模式。这些模式可分为强正相关、强负相关、弱正相关、弱负相关、复杂相关或无相关性。
  4. 现实世界中的例子：在整个教程中，我们提供了现实世界中的例子来说明每种相关性模式。从研究学生身高与臂长，到分析学习时间与考试成绩之间的关系，我们看到了散点图在各个领域中的应用。
  5. 预测能力：散点图使我们能够基于一个变量对另一个变量进行预测，为决策制定和理解因果关系提供有价值的洞察。
  6. 复杂数据：散点图是多功能工具，能够处理复杂数据，包括变量间关系不直接的情况。
  7. 数据解读：能够解读散点图对于研究人员、分析师以及任何希望从数据中得出有意义结论的人来说都至关重要。
  8. 实际应用：散点图在经济学、社会科学、自然科学、工程学等多个领域都有广泛应用。它们有助于识别数据集中的趋势、相关性和异常值。

通过掌握创建、分析和解读散点图的技巧，您将获得一项在数据驱动决策中极为宝贵的技能。无论您是学生、研究人员还是专业人士，散点图都是您数据分析工具箱中的重要工具，能够提供推动明智决策和深化领域理解的洞察。