آموزش نمودار پراکنده: راهنمای سریع
مقدمه
در حوزه تحلیل و نمایش دادهها، نمودارهای پراکنده به عنوان ابزارهای بیقیمتی برای کشف روابط بین متغیرها عمل میکنند. در مورد خاص ما، یک نمودار پراکنده ایجاد کردهایم که به بررسی ارتباط جالب بین طول بازو و قد در میان گروهی از دانشآموزان پایه یازدهم میپردازد. این نمایش بصری دادهها که از هشت نقطه داده منفرد تشکیل شده است، به ما امکان میدهد تا به پویایی بین این دو ویژگی بپردازیم. با بررسی الگوها در نمودار پراکنده، میتوانیم شروع به پیشبینی طول بازو بر اساس قد و قد بر اساس طول بازو کنیم. این تحلیل نه تنها نوری بر ویژگیهای فیزیکی این دانشآموزان میاندازد، بلکه قدرت نمودارهای پراکنده را در روشن کردن همبستگیها نشان میدهد.
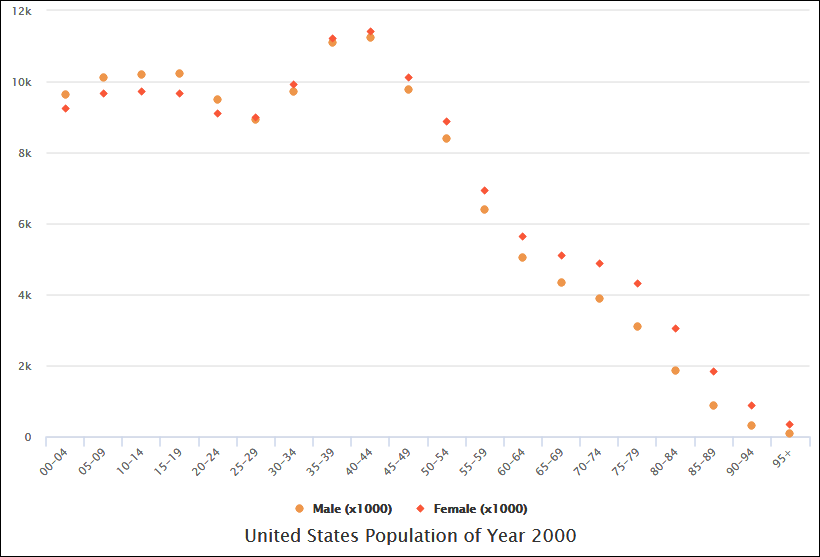
نمودار پراکنده چیست؟
یک نمودار پراکنده، که به عنوان نمودار پراکنده یا نمودار نقطهای نیز شناخته میشود، نوعی نمایش دادهها است که برای نمایش رابطه بین دو متغیر استفاده میشود. هر نقطه در نمودار نماینده یک نقطه داده منفرد است و موقعیت آن توسط مقادیر دو متغیر تعیین میشود. نمودارهای پراکنده برای شناسایی الگوها، روندها و همبستگیهای موجود در دادهها مفید هستند. در زیر، توضیح جامعی درباره نمودارهای پراکنده و مثالهایی برای نشان دادن کاربرد آنها ارائه خواهم کرد.
اجزای یک نمودار پراکنده:
- محور X:محور افقی نماینده یکی از متغیرهای مورد تحلیل است.
- محور Y:محور عمودی نماینده متغیر دیگری است که مورد تحلیل قرار گرفته است.
- نقطههای داده:هر نقطه داده در نمودار نماینده یک مشاهده یا جفت داده منفرد است که یک مقدار برای متغیر محور X و مقدار دیگری برای متغیر محور Y دارد.
- عنوان:عنوانی در بالای نمودار، زمینه و اطلاعاتی درباره محتوای نمودار ارائه میدهد.
- برچسبهای محورها:برچسبهای موجود روی محورهای X و Y اطلاعاتی درباره واحدها یا دستهبندیهای متغیرها ارائه میدهند.
- légende:اگر چندین مجموعه داده در یک نمودار نمایش داده شوند، ممکن است از یک لégende برای تمایز آنها استفاده شود.
مثالهایی از نمودارهای پراکنده:
نمودارهای پراکنده الگوهای مختلفی از همبستگی را نشان میدهند که هر کدام به ارتباط بین مقادیر X و Y اشاره دارند. برای نشان دادن این الگوها، مثالهایی برای هر کدام ارائه میکنیم:
- همبستگی مثبت قوی:
- تعریف:مقدار Y با افزایش مقدار X افزایش مییابد.
- مثال:در یک مطالعه روی تعداد ساعتهای مطالعه و نمرات امتحان، با افزایش تعداد ساعتهای مطالعه (X)، نمرات امتحان (Y) نیز افزایش مییابد. این امر نشاندهنده همبستگی مثبت قوی است.
- همبستگی منفی قوی:
- تعریف:مقدار Y با افزایش مقدار X کاهش مییابد.
- مثال:در یک مطالعه در مورد میزان بارش باران و تعداد ساعتهایی که افراد در فضای باز سپری میکنند، هرچه میزان بارش (X) افزایش مییابد، تعداد ساعتهای گذرانده شده در فضای باز (Y) کاهش مییابد. این موضوع نشاندهنده همبستگی منفی قوی است.
- همبستگی مثبت ضعیف:
- تعریف:مقدار Y به طور خفیف افزایش مییابد هرچه مقدار X افزایش مییابد.
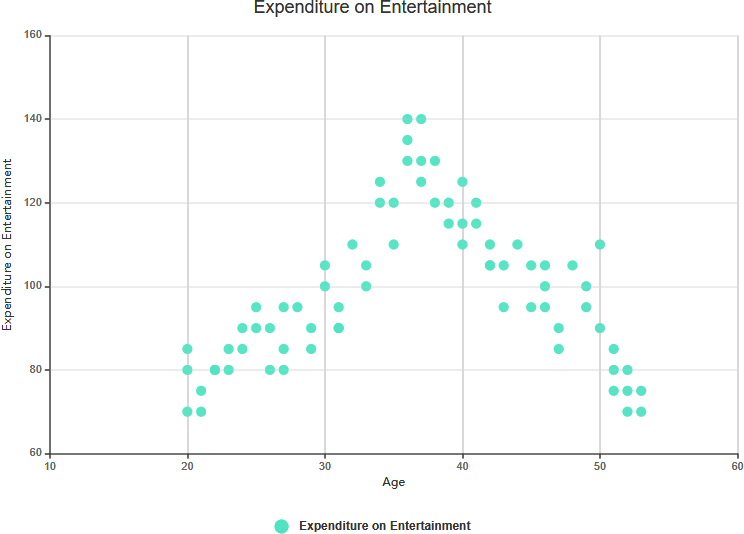
- مثال:با تحلیل سن افراد و درآمد سالانه آنها، ممکن است متوجه شوید که هرچه سن (X) افزایش مییابد، درآمد (Y) به طور خفیف افزایش مییابد. این موضوع نشاندهنده همبستگی مثبت ضعیف است.
- همبستگی منفی ضعیف:
- تعریف:مقدار Y به طور خفیف کاهش مییابد هرچه مقدار X افزایش مییابد.
- مثال:با مطالعه زمان گذرانده شده در سفر به محل کار و سطح انرژی، ممکن است متوجه شوید که هرچه زمان سفر (X) به طور خفیف افزایش مییابد، سطح انرژی (Y) به طور خفیف کاهش مییابد. این موضوع نشاندهنده همبستگی منفی ضعیف است.
- همبستگی پیچیده:
- تعریف:مقدار Y به نظر میرسد با مقدار X مرتبط باشد، اما رابطه به راحتی قابل تعیین نیست.
- مثال:در تحلیل هزینههای تبلیغات و فروش محصولات، رابطه بین این دو ممکن است پیچیده به نظر برسد، با نوسانات و جهت مشخصی نداشته باشد.
- هیچ همبستگی:
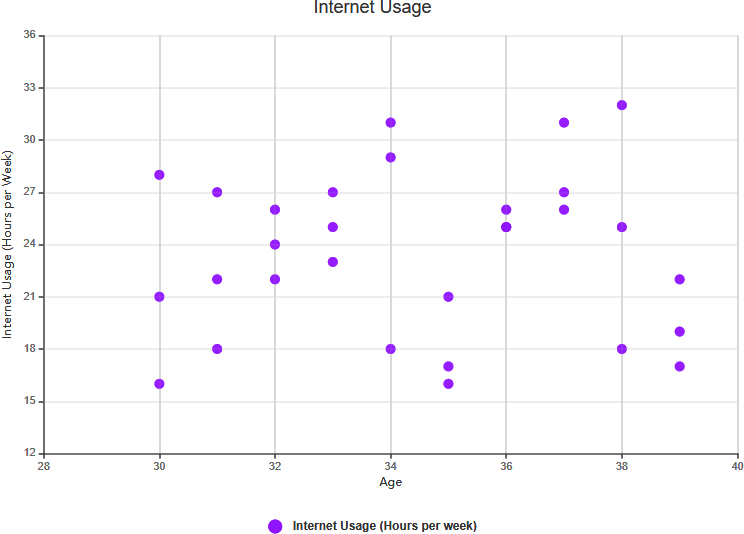
- تعریف:هیچ ارتباطی بین دو متغیر به طور مشخص نشان داده نشده است.
- مثال:اگر اندازه کفش و نمره هوشی را بررسی کنید، ممکن است متوجه شوید که بین آنها رابطه معناداری وجود ندارد. در این حالت، هیچ همبستگی وجود ندارد.
درک این الگوهای همبستگی برای تفسیر نمودارهای پراکندگی و استخراج نتایج معنادار از دادهها ضروری است. تحلیل همبستگی به پیشبینی، درک روابط علّی، و شناسایی روندها در زمینههای مختلفی مانند اقتصاد، علوم اجتماعی و علوم طبیعی کمک میکند.
همبستگی مثبت قوی
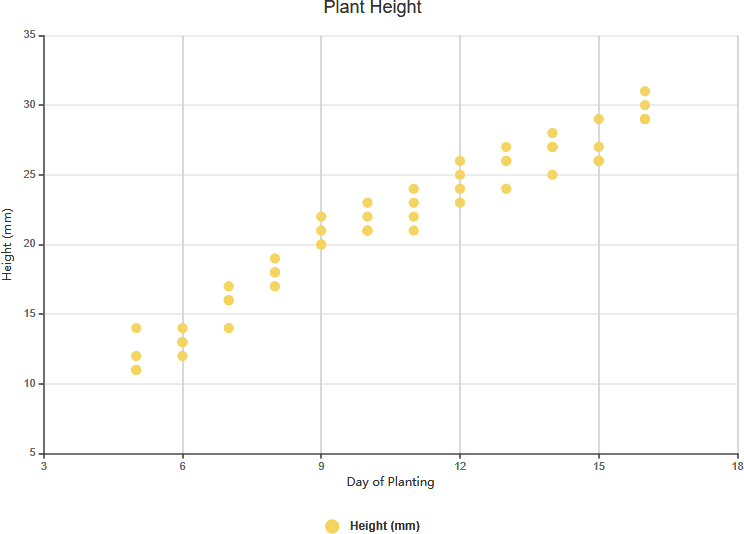
همبستگی منفی قوی
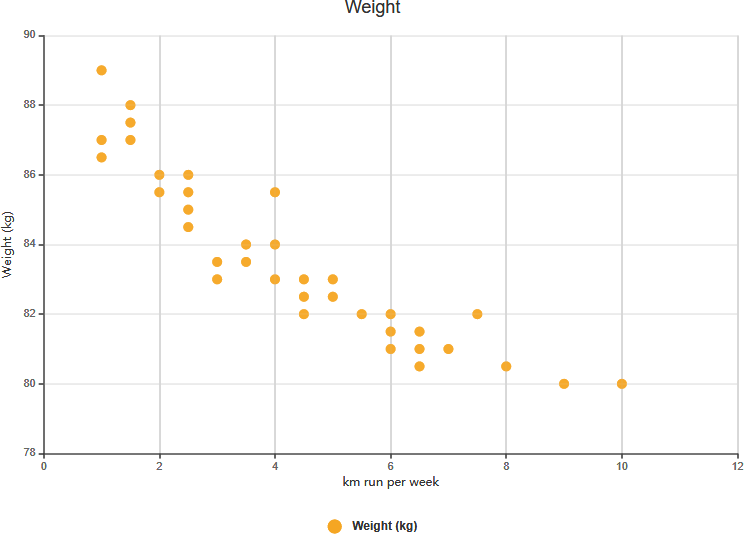
همبستگی مثبت ضعیف
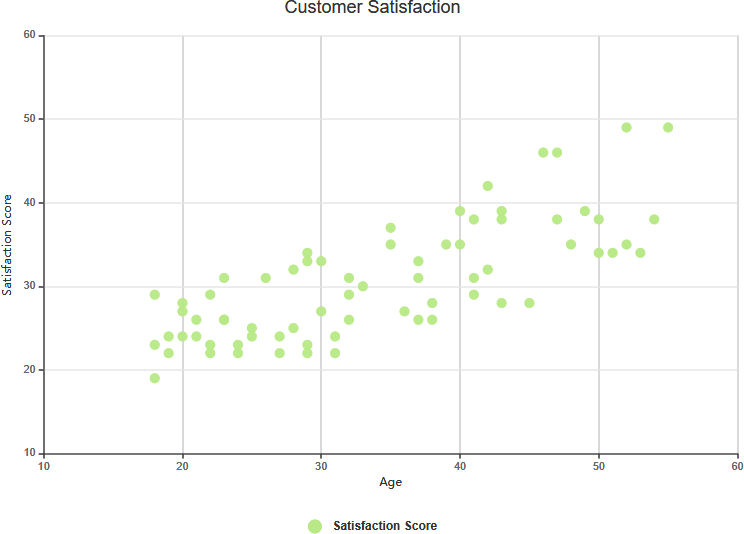
همبستگی پیچیده
هیچ ارتباطی وجود ندارد
مثال نمودار پراکنده: طول بازو در مقابل پایه یازدهم
نمودار پراکنده بالا دادههای مربوط به قد و طول بازو هشت دانشآموز پایه یازدهم را نشان میدهد. با بررسی رابطه بین قد و طول بازوی یک دانشآموز، میتوانیم روندی را تشخیص دهیم. این روند به ما امکان میدهد طول بازوی یک دانشآموز را بر اساس قد داده شده و برعکس، تخمین بزنیم. در این نمودار خاص، ارتباط مثبت بین طول بازو و قد به وضوح مشهود است.
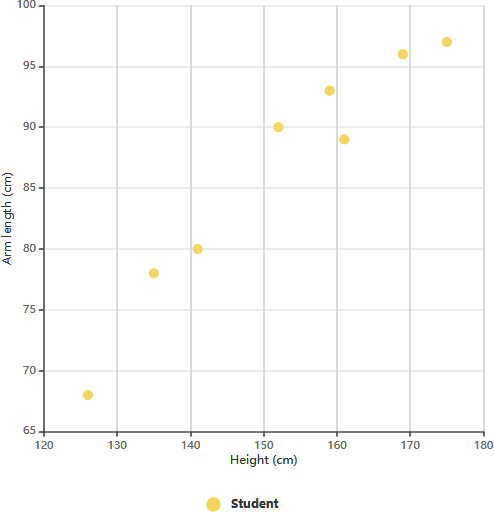
پس از برقراری ارتباط بین این متغیرها، میتوانیم پیشبینیهایی درباره رفتار متغیر وابسته با استفاده از اندازهگیری متغیر مستقل انجام دهیم. این نمودار به ویژه زمانی ارزشمند است که یکی از متغیرها آسان برای اندازهگیری باشد در حالی که دیگری نیست. به عنوان مثال، اگر یک دانشآموز پایه یازدهم قد ۱۴۸ سانتیمتر داشته باشد، میتوانیم تخمین بزنیم که طول بازوی او حدود ۸۴ سانتیمتر است.
نتیجهگیری
در این نمودار پراکنده، ما مبانی نمودارهای پراکنده و نقش اساسی آنها در بصریسازی و تحلیل دادهها را بررسی کردیم. نمودارهای پراکنده ابزاری قدرتمند برای نمایش روابط بین متغیرها و کشف الگوها در دادهها فراهم میکنند. بیایید برخی از نکات کلیدی این آموزش را مرور کنیم:
- تعریف نمودارهای پراکنده:نمودارهای پراکنده، که به آنها نمودارهای پراکنده یا نمودارهای پراکنده نیز گفته میشود، نقاط داده را در یک صفحه دو بعدی نمایش میدهند، به طوری که هر نقطه نماینده یک مشاهده یا جفت داده منحصر به فرد است.
- متغیرها و محورها:نمودارهای پراکنده معمولاً از دو محور تشکیل شدهاند: محور X و محور Y. این محورها متغیرهای مورد مطالعه را نمایش میدهند و امکان بصریسازی اینکه تغییرات در یک متغیر چگونه با تغییرات در متغیر دیگر مرتبط است را فراهم میکنند.
- الگوهای همبستگی:نمودارهای پراکنده به ما کمک میکنند تا الگوهای مختلف همبستگی بین متغیرها را شناسایی کنیم. این الگوها میتوانند به صورت همبستگی مثبت قوی، همبستگی منفی قوی، همبستگی مثبت ضعیف، همبستگی منفی ضعیف، همبستگی پیچیده یا هیچ همبستگی طبقهبندی شوند.
- مثالهای دنیای واقعی:در طول آموزش، ما مثالهای واقعی را ارائه کردیم تا هر یک از این الگوهای همبستگی را توضیح دهیم. از مطالعه قد و طول بازوی دانشآموزان تا تحلیل رابطه بین ساعات مطالعه و نمرات امتحان، دیدیم که چگونه نمودارهای پراکنده میتوانند در حوزههای مختلفی کاربرد داشته باشند.
- توانایی پیشبینی:نمودارهای پراکنده به ما امکان میدهند بر اساس یک متغیر، پیشبینیهایی درباره متغیر دیگر انجام دهیم، که این امر به تصمیمگیری و درک روابط علّی ارزشمندی فراهم میکند.
- دادههای پیچیده:نمودارهای پراکنده ابزارهای چندمنظورهای هستند که میتوانند با دادههای پیچیده کار کنند، از جمله مواردی که رابطه بین متغیرها ساده و مستقیم نباشد.
- تفسیر دادهها:توانایی تفسیر نمودارهای پراکنده برای محققان، تحلیلگران و هر کسی که بخواهد نتایج معناداری از دادهها استخراج کند، حیاتی است.
- کاربردهای عملی:نمودارهای پراکنده کاربردهایی در زمینههای متنوعی مانند اقتصاد، علوم اجتماعی، علوم طبیعی، مهندسی و غیره دارند. آنها در شناسایی روندها، همبستگیها و نقاط بینظیر در مجموعه دادهها کمک میکنند.
با تسلط بر هنر ایجاد، تحلیل و تفسیر نمودارهای پراکنده، خود را با مهارتی ارزشمند برای تصمیمگیری مبتنی بر دادهها تجهیز میکنید. چه دانشآموز باشید، چه محقق یا فرد حرفهای، نمودارهای پراکنده ابزاری ارزشمند در ابزارهای تحلیل داده شما هستند و بینشهایی فراهم میکنند که میتوانند تصمیمگیریهای آگاهانه و درک عمیقتری در حوزه مورد علاقه شما را تسهیل کنند.

















