Un tutoriel sur les diagrammes de dispersion : un guide rapide

Introduction

Dans le domaine de l’analyse et de la visualisation des données, les diagrammes de dispersion constituent des outils inestimables pour découvrir les relations entre les variables. Dans notre cas particulier, nous avons créé un diagramme de dispersion qui explore la relation fascinante entre la longueur du bras et la taille chez un groupe d’élèves de première année secondaire. Cette représentation visuelle des données, composée de huit points de données individuels, nous permet d’explorer les dynamiques entre ces deux caractéristiques. En étudiant les motifs présents dans le diagramme de dispersion, nous pouvons commencer à faire des prévisions sur la longueur du bras en fonction de la taille, et inversement. Cette analyse éclaire non seulement les caractéristiques physiques de ces élèves, mais démontre également la puissance des diagrammes de dispersion pour révéler des corrélations.

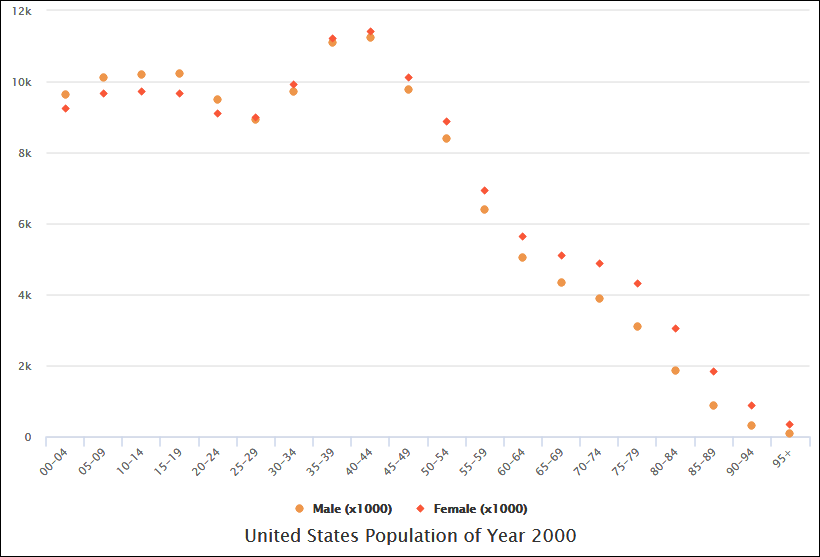
Qu’est-ce qu’un diagramme de dispersion

Un diagramme de dispersion, également connu sous le nom de diagramme de dispersion ou graphique de dispersion, est un type de visualisation de données utilisé pour afficher la relation entre deux variables. Chaque point du graphique représente un point de données unique, et la position du point est déterminée par les valeurs des deux variables. Les diagrammes de dispersion sont utiles pour identifier des motifs, des tendances et des corrélations dans les données. Ci-dessous, je fournirai une explication complète des diagrammes de dispersion et des exemples pour illustrer leur utilisation.

Composants d’un diagramme de dispersion :

1. Axe des abscisses : L’axe horizontal représente l’une des variables analysées.
2. Axe des ordonnées : L’axe vertical représente l’autre variable analysée.
3. Points de données : Chaque point de données sur le graphique représente une observation unique ou une paire de données, avec une valeur pour la variable de l’axe des abscisses et une autre pour la variable de l’axe des ordonnées.
4. Titre : Un titre en haut du graphique fournit un contexte et des informations sur ce que représente le graphique.
5. Étiquettes des axes : Les étiquettes de l’axe des abscisses et de l’axe des ordonnées fournissent des informations sur les unités ou les catégories des variables.
6. Légende : Si plusieurs jeux de données sont affichés sur le même graphique, une légende peut être utilisée pour les distinguer.

Exemples de diagrammes de dispersion :

1. Corrélation positive forte :
   • Définition : La valeur de Y augmente lorsque la valeur de X augmente.
   • Exemple : Dans une étude du nombre d’heures passées à étudier et des résultats aux examens, à mesure que le nombre d’heures passées à étudier (X) augmente, les résultats aux examens (Y) augmentent également. Cela indique une forte corrélation positive.
2. Corrélation négative forte :
   • Définition : La valeur de Y diminue lorsque la valeur de X augmente.
   • Exemple :Dans une étude portant sur la quantité de pluie et le nombre d’heures passées à l’extérieur, à mesure que la quantité de pluie (X) augmente, le nombre d’heures passées à l’extérieur (Y) diminue. Cela démontre une forte corrélation négative.
3. Corrélation positive faible :
   • Définition :La valeur de Y augmente légèrement lorsque la valeur de X augmente.
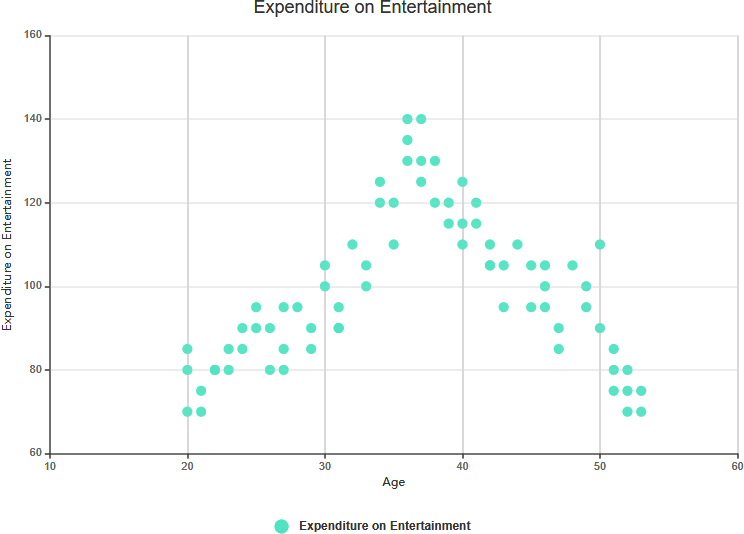
   • Exemple :En analysant l’âge des individus et leur revenu annuel, vous pourriez constater que, à mesure que l’âge (X) augmente, le revenu (Y) augmente légèrement. Cela indique une corrélation positive faible.
4. Corrélation négative faible :
   • Définition :La valeur de Y diminue légèrement lorsque la valeur de X augmente.
   • Exemple :En étudiant le temps passé à se rendre au travail et les niveaux d’énergie, vous pourriez remarquer que, à mesure que le temps de trajet (X) augmente légèrement, les niveaux d’énergie (Y) diminuent légèrement. Cela suggère une corrélation négative faible.
5. Corrélation complexe :
   • Définition :La valeur de Y semble être liée à la valeur de X, mais la relation n’est pas facile à déterminer.
   • Exemple :Dans une analyse des dépenses publicitaires et des ventes de produits, la relation entre les deux peut sembler complexe, avec des fluctuations et aucune direction claire.
6. Pas de corrélation :
   • Définition :Il n’y a pas de lien démontré entre les deux variables.
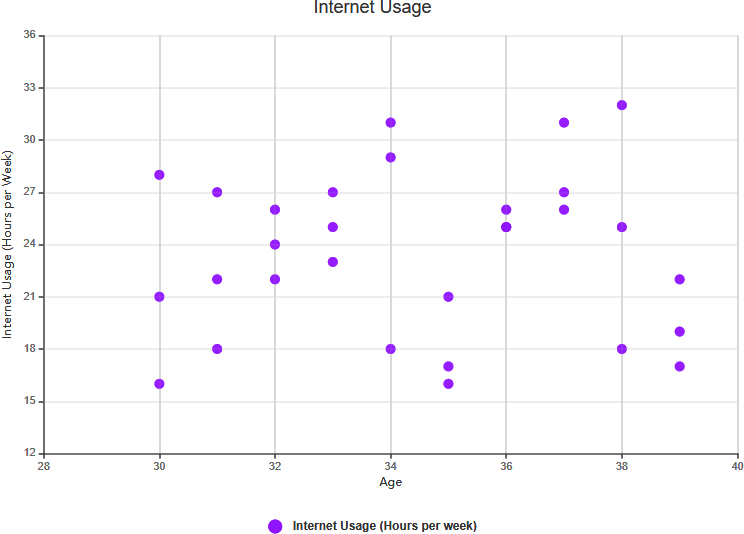
   • Exemple :Si vous examinez la pointure et les scores d’intelligence, vous pourriez constater qu’il n’y a pas de relation significative entre les deux. Dans ce cas, il n’y a pas de corrélation.

Comprendre ces modèles de corrélation est essentiel pour interpréter les diagrammes de dispersion et tirer des conclusions significatives à partir des données. L’analyse de corrélation aide à faire des prévisions, à comprendre les relations de cause à effet, et à identifier les tendances dans divers domaines tels que l’économie, les sciences sociales et les sciences naturelles.

Corrélation positive forte

Modifier ce diagramme

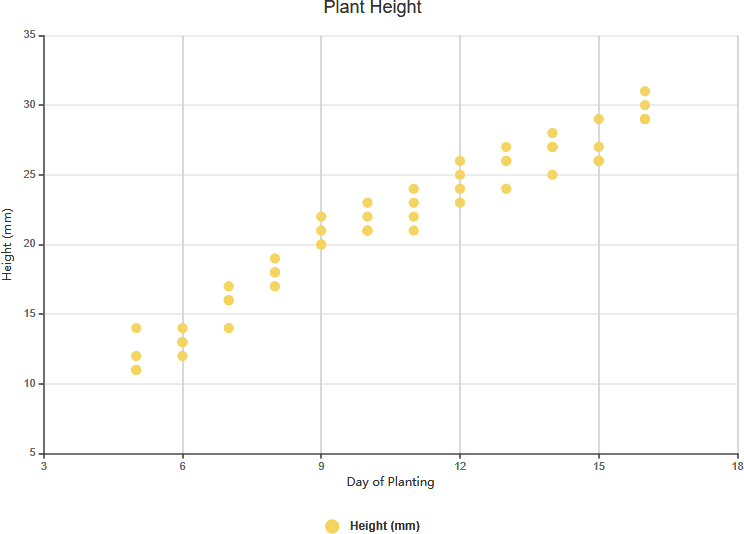
Corrélation négative forte

Modifier ce diagramme

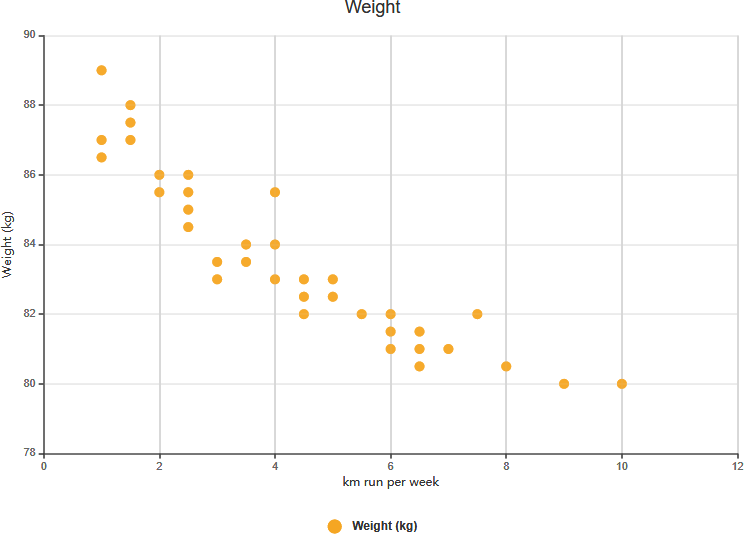
Corrélation positive faible

Modifier ce diagramme

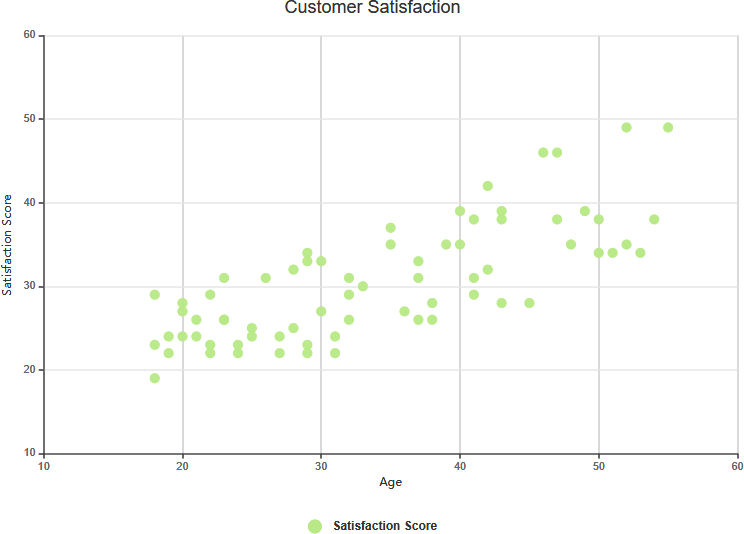
Corrélation complexe

Modifier ce diagramme

Pas de corrélation

Modifier ce diagramme

Exemple de diagramme en nuage de points : Longueur du bras par rapport à la 11e année

Le nuage de points ci-dessus illustre les données relatives à la taille et à la longueur du bras de huit élèves de 11e année. En examinant la relation entre la taille d’un élève et sa longueur du bras, nous pouvons identifier une tendance. Cette tendance nous permet d’estimer la longueur du bras d’un élève en fonction de sa taille donnée, et inversement. Dans ce graphique particulier, une corrélation positive entre la longueur du bras et la taille est évidente.

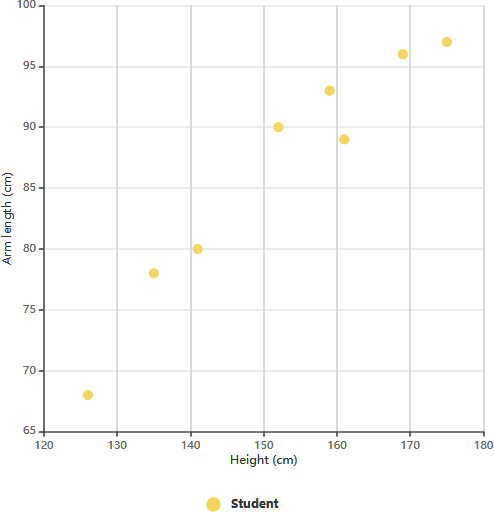
Après avoir établi la corrélation entre ces variables, nous pouvons faire des prévisions sur le comportement de la variable dépendante à l’aide des mesures de la variable indépendante. Ce graphique s’avère particulièrement utile lorsque l’une des variables est facile à mesurer tandis que l’autre ne l’est pas. Par exemple, si un élève de 11e année mesure 148 cm, nous pouvons estimer que sa longueur du bras est d’environ 84 cm.

Conclusion

Dans ce diagramme en nuage de points, nous avons exploré les fondamentaux des diagrammes en nuage de points et leur rôle essentiel dans la visualisation et l’analyse des données. Les diagrammes en nuage de points offrent un moyen puissant de représenter les relations entre les variables et de découvrir des motifs dans les données. Récapitulons quelques points clés de ce tutoriel :

1. Définition des diagrammes en nuage de points :Les diagrammes en nuage de points, également appelés diagrammes de dispersion ou graphiques de dispersion, affichent des points de données sur un plan à deux dimensions, chaque point représentant une observation unique ou une paire de données.
2. Variables et axes :Les diagrammes en nuage de points comprennent généralement deux axes : l’axe des abscisses (X) et l’axe des ordonnées (Y). Ces axes représentent les variables étudiées, permettant de visualiser comment les variations d’une variable se rapportent aux variations de l’autre.
3. Schémas de corrélation :Les diagrammes en nuage de points nous aident à identifier différents schémas de corrélation entre les variables. Ces schémas peuvent être classés comme une forte corrélation positive, une forte corrélation négative, une faible corrélation positive, une faible corrélation négative, une corrélation complexe ou aucune corrélation.
4. Exemples du monde réel :Tout au long du tutoriel, nous avons fourni des exemples du monde réel pour illustrer chacun de ces schémas de corrélation. Que ce soit en étudiant la taille des élèves et la longueur du bras, ou en analysant la relation entre les heures d’étude et les résultats aux examens, nous avons vu comment les diagrammes en nuage de points peuvent être appliqués dans divers domaines.
5. Pouvoir prédictif :Les diagrammes en nuage de points nous permettent de faire des prévisions sur une variable en fonction de l’autre, offrant des informations précieuses pour la prise de décision et la compréhension des relations causales.
6. Données complexes :Les diagrammes en nuage de points sont des outils polyvalents capables de gérer des données complexes, y compris dans les situations où la relation entre les variables n’est pas directe.
7. Interprétation des données :La capacité à interpréter les diagrammes en nuage de points est essentielle pour les chercheurs, les analystes et toute personne souhaitant tirer des conclusions significatives à partir des données.
8. Applications pratiques :Les diagrammes en nuage de points trouvent des applications dans des domaines aussi variés que l’économie, les sciences sociales, les sciences naturelles, l’ingénierie, et bien d’autres. Ils aident à identifier les tendances, les corrélations et les valeurs aberrantes au sein des jeux de données.

En maîtrisant l’art de créer, d’analyser et d’interpréter les diagrammes en nuage de points, vous vous munissez d’une compétence précieuse pour la prise de décisions fondées sur les données. Que vous soyez étudiant, chercheur ou professionnel, les diagrammes en nuage de points constituent un outil précieux dans votre arsenal d’analyse de données, offrant des perspectives qui peuvent guider des choix éclairés et favoriser une compréhension plus profonde dans votre domaine d’expertise.