Tutorial de gráfico de dispersión: Una guía rápida
Introducción
En el ámbito del análisis y visualización de datos, los gráficos de dispersión son herramientas invaluables para descubrir relaciones entre variables. En nuestro caso particular, hemos generado un gráfico de dispersión que explora la intrigante conexión entre la longitud del brazo y la estatura entre un grupo de estudiantes de undécimo grado. Esta representación visual de datos, compuesta por ocho puntos de datos individuales, nos permite profundizar en las dinámicas entre estos dos atributos. Al estudiar los patrones dentro del gráfico de dispersión, podemos comenzar a hacer predicciones sobre la longitud del brazo en función de la estatura y viceversa. Este análisis no solo ilumina las características físicas de estos estudiantes, sino que también demuestra el poder de los gráficos de dispersión para revelar correlaciones.
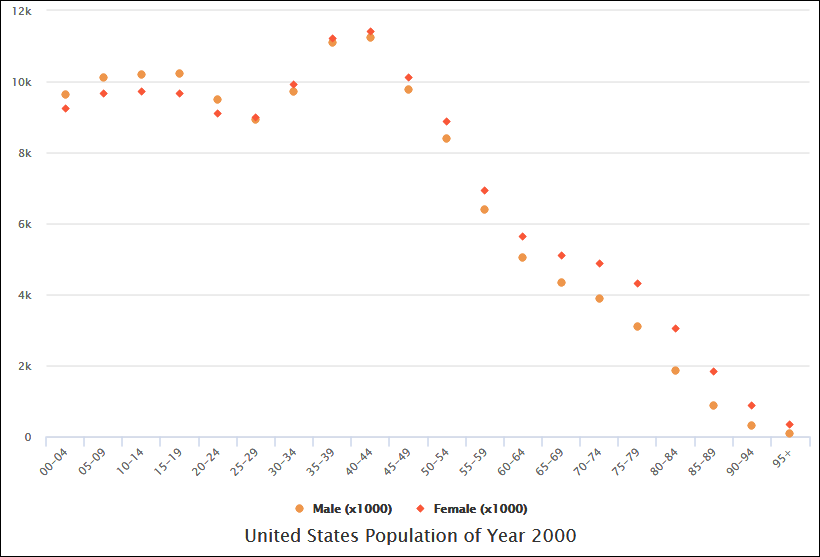
¿Qué es un gráfico de dispersión
Un gráfico de dispersión, también conocido como gráfico de dispersión o gráfico de puntos, es un tipo de visualización de datos utilizado para mostrar la relación entre dos variables. Cada punto en el gráfico representa un único punto de datos, y la posición del punto se determina por los valores de las dos variables. Los gráficos de dispersión son útiles para identificar patrones, tendencias y correlaciones en los datos. A continuación, proporcionaré una explicación completa sobre los gráficos de dispersión y ejemplos para ilustrar su uso.
Componentes de un gráfico de dispersión:
- Eje X: El eje horizontal representa una de las variables que se analizan.
- Eje Y: El eje vertical representa la otra variable que se analiza.
- Puntos de datos: Cada punto de datos en el gráfico representa una observación individual o un par de datos, con un valor para la variable del eje X y otro para la variable del eje Y.
- Título: Un título en la parte superior del gráfico proporciona contexto e información sobre lo que representa el gráfico.
- Etiquetas de los ejes: Las etiquetas del eje X y el eje Y proporcionan información sobre las unidades o categorías de las variables.
- Leyenda: Si se muestran múltiples conjuntos de datos en el mismo gráfico, puede usarse una leyenda para diferenciarlos.
Ejemplos de gráficos de dispersión:
Los gráficos de dispersión muestran diversos patrones de correlación, cada uno reflejando la conexión entre los valores de X e Y. Para ilustrar estos patrones, proporcionaremos ejemplos para cada uno:
- Correlación positiva fuerte:
- Definición: El valor de Y aumenta a medida que aumenta el valor de X.
- Ejemplo: En un estudio sobre el número de horas dedicadas al estudio y las calificaciones en los exámenes, a medida que aumenta el número de horas dedicadas al estudio (X), también aumentan las calificaciones en los exámenes (Y). Esto indica una correlación positiva fuerte.
- Correlación negativa fuerte:
- Definición: El valor de Y disminuye a medida que aumenta el valor de X.
- Ejemplo:En un estudio sobre la cantidad de lluvia y el número de horas que las personas pasan al aire libre, a medida que aumenta la cantidad de lluvia (X), el número de horas al aire libre (Y) disminuye. Esto demuestra una fuerte correlación negativa.
- Correlación positiva débil:
- Definición:El valor de Y aumenta ligeramente a medida que aumenta el valor de X.
- Ejemplo:Al analizar la edad de las personas y sus ingresos anuales, podrías encontrar que a medida que aumenta la edad (X), los ingresos (Y) aumentan ligeramente. Esto indica una correlación positiva débil.
- Correlación negativa débil:
- Definición:El valor de Y disminuye ligeramente a medida que aumenta el valor de X.
- Ejemplo:Al estudiar la cantidad de tiempo dedicado al desplazamiento al trabajo y los niveles de energía, podrías notar que a medida que aumenta ligeramente el tiempo de desplazamiento (X), los niveles de energía (Y) disminuyen ligeramente. Esto sugiere una correlación negativa débil.
- Correlación compleja:
- Definición:El valor de Y parece estar relacionado con el valor de X, pero la relación no es fácil de determinar.
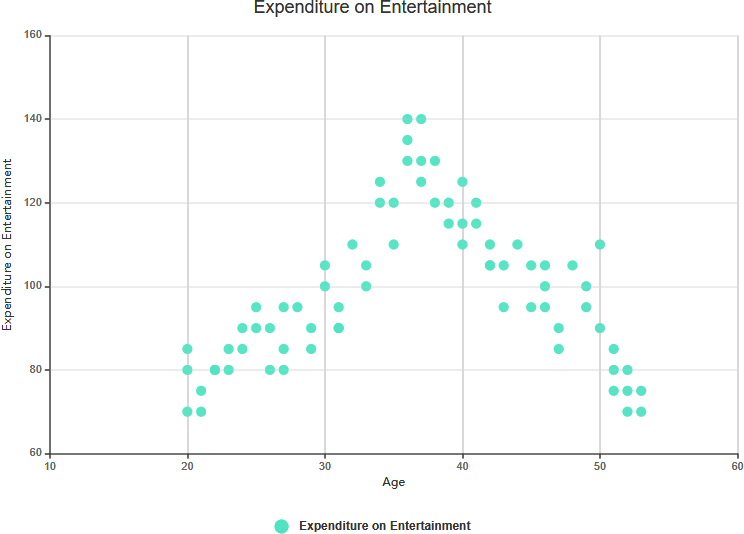
- Ejemplo:En un análisis del gasto en publicidad y las ventas de productos, la relación entre ambos puede parecer compleja, con fluctuaciones y sin una dirección clara.
- Sin correlación:
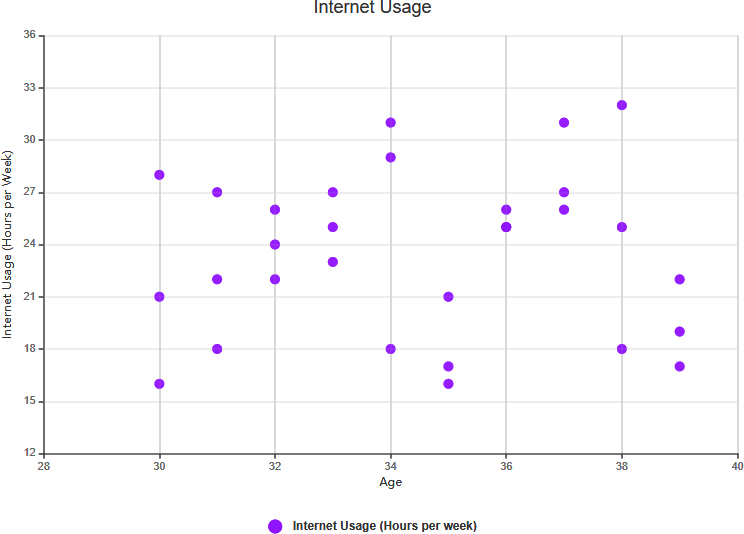
- Definición:No hay una conexión demostrada entre las dos variables.
- Ejemplo:Si examinas el tamaño de calzado y los puntajes de CI, podrías encontrar que no hay una relación significativa entre ellos. En este caso, no hay correlación.
Comprender estos patrones de correlación es esencial para interpretar los gráficos de dispersión y extraer conclusiones significativas a partir de los datos. El análisis de correlación ayuda a hacer predicciones, comprender las relaciones de causa y efecto, y identificar tendencias en diversos campos como la economía, las ciencias sociales y las ciencias naturales.
Correlación positiva fuerte
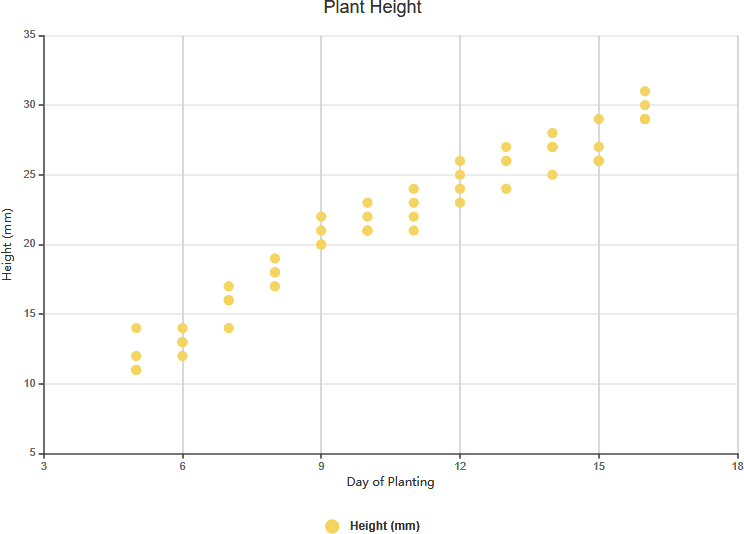
Correlación negativa fuerte
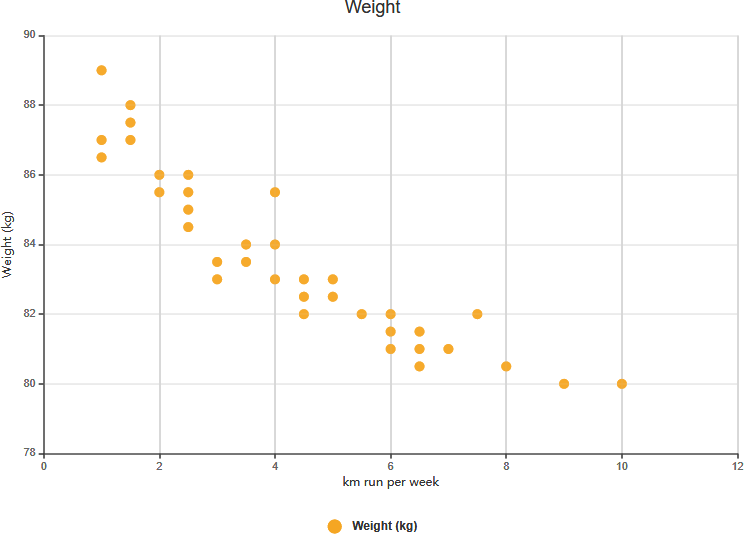
Correlación positiva débil
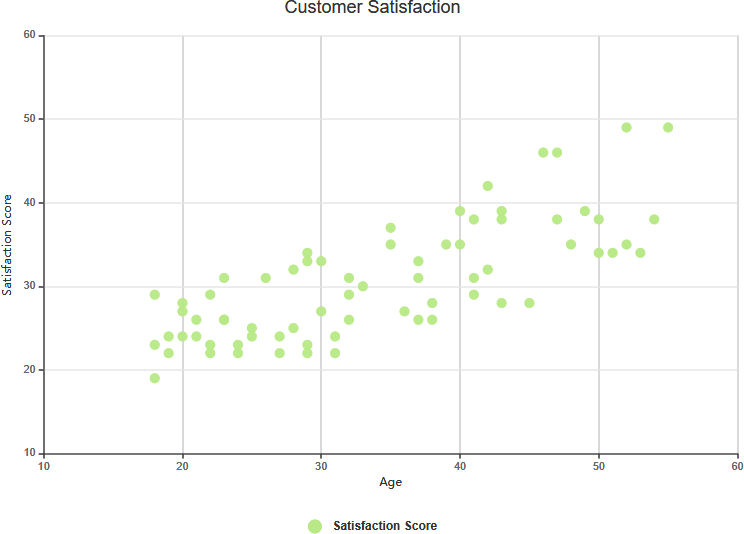
Correlación compleja
Sin correlación
Ejemplo de gráfico de dispersión: Longitud del brazo frente a grado 11
El gráfico de dispersión anterior ilustra datos sobre la altura y la longitud del brazo de ocho estudiantes de grado 11. Al examinar la relación entre la altura y la longitud del brazo de un estudiante, podemos identificar una tendencia. Esta tendencia nos permite estimar la longitud del brazo de un estudiante según su altura dada, y viceversa. En este gráfico en particular, es evidente una correlación positiva entre la longitud del brazo y la altura.
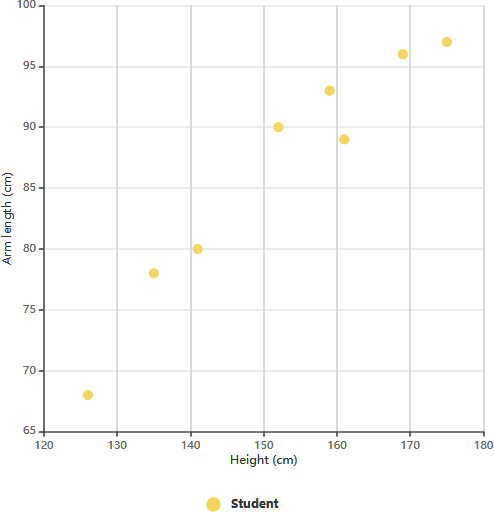
Después de establecer la correlación entre estas variables, podemos hacer predicciones sobre el comportamiento de la variable dependiente utilizando las mediciones de la variable independiente. Este gráfico resulta particularmente valioso cuando una de las variables es fácil de medir mientras que la otra no lo es. Por ejemplo, si un estudiante de grado 11 tiene una altura de 148 cm, podemos estimar que su longitud del brazo es aproximadamente de 84 cm.
Conclusión
En este gráfico de dispersión, hemos explorado los fundamentos de los gráficos de dispersión y su papel esencial en la visualización y análisis de datos. Los gráficos de dispersión ofrecen una herramienta poderosa para representar relaciones entre variables y descubrir patrones dentro de los datos. Repasemos algunos puntos clave de este tutorial:
- Definición de gráficos de dispersión:Los gráficos de dispersión, también conocidos como gráficos de dispersión o gráficos de puntos, muestran puntos de datos en un plano bidimensional, donde cada punto representa una observación única o un par de datos.
- Variables y ejes:Los gráficos de dispersión suelen constar de dos ejes: el eje X y el eje Y. Estos ejes representan las variables bajo estudio, lo que permite visualizar cómo los cambios en una variable se relacionan con los cambios en otra.
- Patrones de correlación:Los gráficos de dispersión nos ayudan a identificar diferentes patrones de correlación entre variables. Estos patrones se pueden categorizar como correlación positiva fuerte, correlación negativa fuerte, correlación positiva débil, correlación negativa débil, correlación compleja o sin correlación.
- Ejemplos del mundo real:A lo largo del tutorial, proporcionamos ejemplos del mundo real para ilustrar cada uno de estos patrones de correlación. Desde el estudio de la altura y la longitud del brazo de los estudiantes hasta el análisis de la relación entre las horas de estudio y las calificaciones en los exámenes, vimos cómo los gráficos de dispersión pueden aplicarse en diversos campos.
- Poder predictivo:Los gráficos de dispersión nos permiten hacer predicciones sobre una variable basándonos en la otra, proporcionando información valiosa para la toma de decisiones y la comprensión de relaciones causales.
- Datos complejos:Los gráficos de dispersión son herramientas versátiles que pueden manejar datos complejos, incluyendo situaciones en las que la relación entre las variables no es directa.
- Interpretación de datos:La capacidad de interpretar gráficos de dispersión es crucial para investigadores, analistas y cualquier persona que busque extraer conclusiones significativas de los datos.
- Aplicaciones prácticas:Los gráficos de dispersión tienen aplicaciones en campos tan diversos como la economía, las ciencias sociales, las ciencias naturales, la ingeniería y muchos más. Ayudan a identificar tendencias, correlaciones y valores atípicos dentro de los conjuntos de datos.
Al dominar el arte de crear, analizar e interpretar gráficos de dispersión, te equipas con una habilidad valiosa para la toma de decisiones basada en datos. Ya seas estudiante, investigador o profesional, los gráficos de dispersión son una herramienta valiosa en tu kit de análisis de datos, ofreciendo perspectivas que pueden impulsar decisiones informadas y una comprensión más profunda en tu campo elegido.

















