Poradnik wykresu rozproszenia: Szybki przewodnik

Wprowadzenie

W dziedzinie analizy danych i wizualizacji wykresy rozproszenia są niezwykle cennymi narzędziami do odkrywania zależności między zmiennymi. W naszym konkretnym przypadku stworzyliśmy wykres rozproszenia, który bada fascynującą zależność między długością ramion a wzrostem wśród grupy uczniów klas jednastych. Ta wizualna prezentacja danych, składająca się z ośmiu indywidualnych punktów danych, pozwala nam zbadać dynamikę między tymi dwoma cechami. Analizując wzory na wykresie rozproszenia, możemy zacząć przewidywać długość ramion na podstawie wzrostu i wzrostu na podstawie długości ramion. Ta analiza nie tylko ujawnia cechy fizyczne tych uczniów, ale również pokazuje moc wykresów rozproszenia w ujawnianiu korelacji.

Co to jest wykres rozproszenia

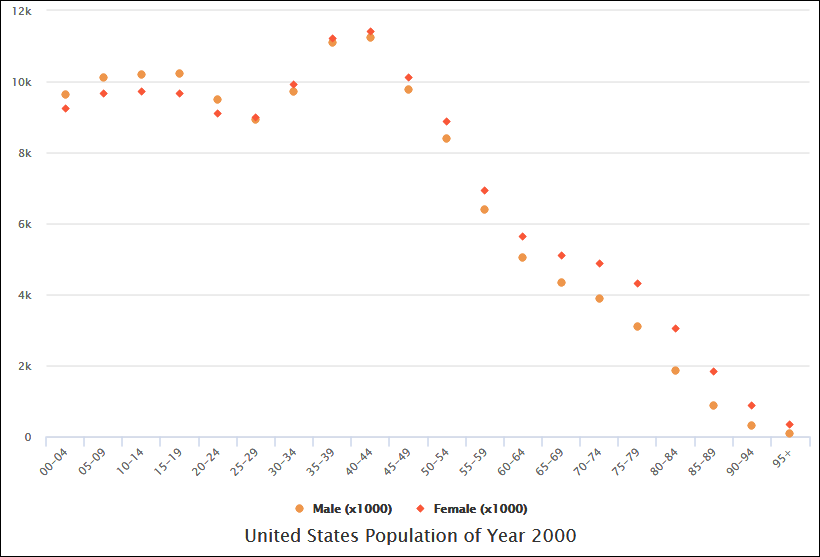
Wykres rozproszenia, znany również jako wykres punktowy lub wykres rozproszenia, to rodzaj wizualizacji danych używany do przedstawienia związku między dwiema zmiennymi. Każdy punkt na wykresie reprezentuje pojedynczy punkt danych, a jego położenie jest określone wartościami tych dwóch zmiennych. Wykresy rozproszenia są pomocne w identyfikowaniu wzorców, trendów i korelacji w danych. Poniżej przedstawię szczegółowe wyjaśnienie wykresów rozproszenia oraz przykłady ilustrujące ich zastosowanie.

Elementy wykresu rozproszenia:

1. Oś X: Oś pozioma reprezentuje jedną z analizowanych zmiennych.
2. Oś Y: Oś pionowa reprezentuje drugą analizowaną zmienną.
3. Punkty danych: Każdy punkt danych na wykresie reprezentuje pojedynczą obserwację lub parę danych, z jedną wartością dla zmiennej osi X i drugą dla zmiennej osi Y.
4. Tytuł: Tytuł umieszczony na górze wykresu dostarcza kontekstu i informacji o tym, co wykres przedstawia.
5. Etykiety osi: Etykiety na osi X i Y dostarczają informacji o jednostkach lub kategoriach zmiennych.
6. Legenda: Jeśli na tym samym wykresie wyświetlone są wiele zestawów danych, legenda może służyć do ich rozróżnienia.

Przykłady wykresów rozproszenia:

1. Silna korelacja dodatnia:
   • Definicja: Wartość Y rośnie wraz ze wzrostem wartości X.
   • Przykład: W badaniu liczby godzin poświęconych na naukę i wyników egzaminów, wraz ze wzrostem liczby godzin poświęconych na naukę (X), wyniki egzaminów (Y) również rosną. Oznacza to silną korelację dodatnią.
2. Silna korelacja ujemna:
   • Definicja: Wartość Y maleje wraz ze wzrostem wartości X.
   • Przykład:W badaniu ilości opadów i liczby godzin spędzanych na zewnątrz przez ludzi, wraz ze wzrostem ilości opadów (X) liczba godzin spędzanych na zewnątrz (Y) maleje. Pokazuje to silną korelację ujemną.
3. Słaba korelacja dodatnia:
   • Definicja:Wartość Y nieznacznie rośnie wraz ze wzrostem wartości X.
   • Przykład:Analizując wiek osób i ich roczne dochody, możesz zauważyć, że wraz ze wzrostem wieku (X) dochód (Y) nieznacznie rośnie. Oznacza to słabą korelację dodatnią.
4. Słaba korelacja ujemna:
   • Definicja:Wartość Y nieznacznie maleje wraz ze wzrostem wartości X.
   • Przykład:Badając czas poświęcony na drogę do pracy i poziom energii, możesz zauważyć, że wraz ze nieznacznym wzrostem czasu przejazdu (X) poziom energii (Y) nieznacznie spada. Wskazuje to na słabą korelację ujemną.
5. Złożona korelacja:
   • Definicja:Wartość Y wydaje się być związana z wartością X, ale relacja nie jest łatwo określona.
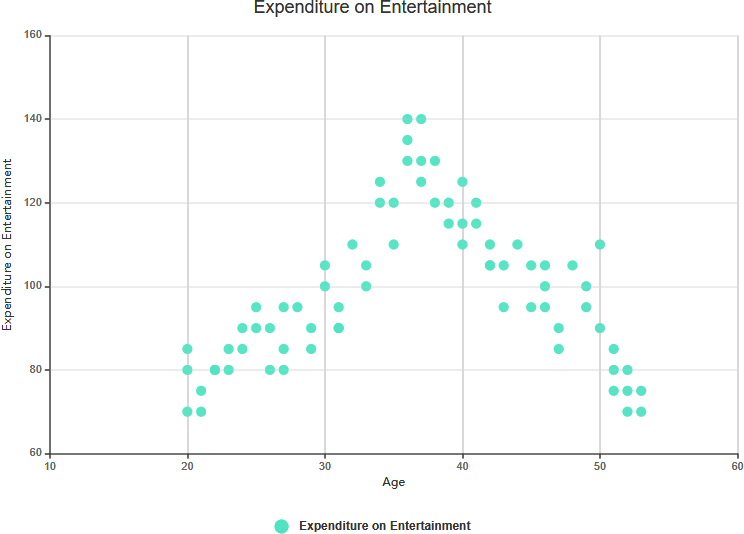
   • Przykład:W analizie wydatków na reklamę i sprzedaży produktów relacja między nimi może wydawać się złożona, z wahaniemi i brakiem jasnego kierunku.
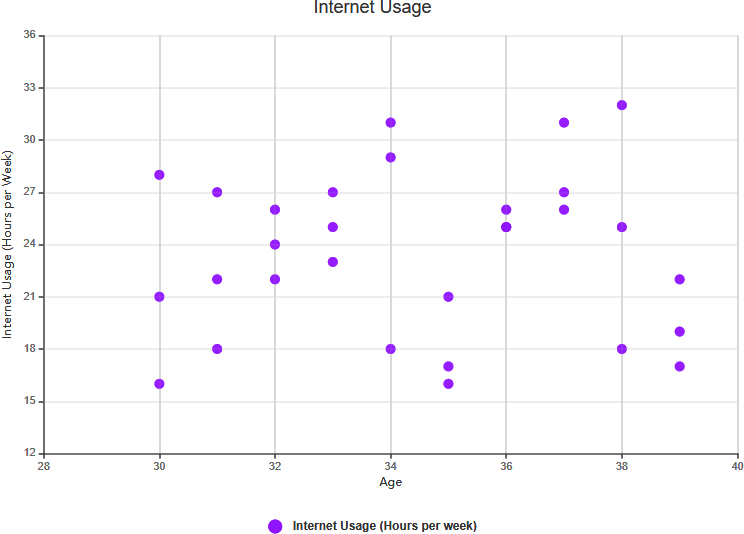
6. Brak korelacji:
   • Definicja:Nie ma wykazanej zależności między tymi zmiennymi.
   • Przykład:Jeśli przeanalizujesz rozmiar butów i wyniki testów inteligencji, możesz stwierdzić, że nie ma istotnej zależności między nimi. W tym przypadku nie ma korelacji.

Zrozumienie tych wzorców korelacji jest kluczowe do interpretacji wykresów rozrzutu i wyciągania istotnych wniosków z danych. Analiza korelacji pomaga w przewidywaniu, zrozumieniu relacji przyczynowo-skutkowych oraz identyfikacji trendów w różnych dziedzinach, takich jak ekonomia, nauki społeczne i nauki przyrodnicze.

Silna korelacja dodatnia

Edytuj ten diagram

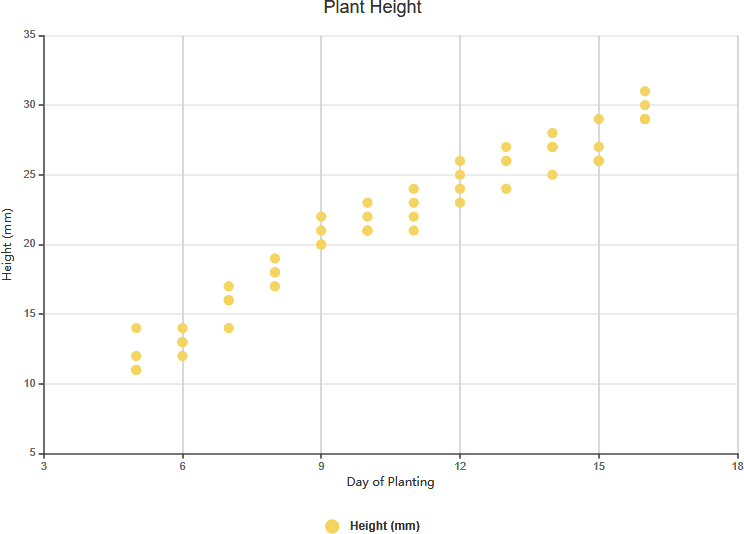
Silna korelacja ujemna

Edytuj ten diagram

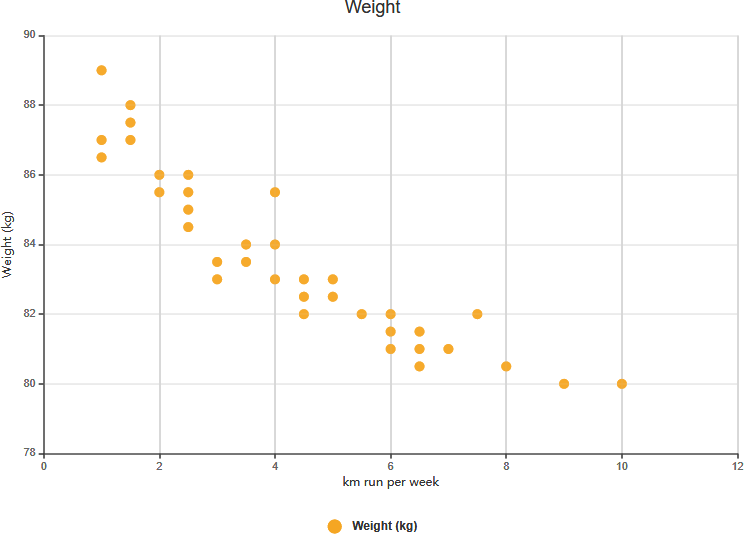
Słaba korelacja dodatnia

Edytuj ten diagram

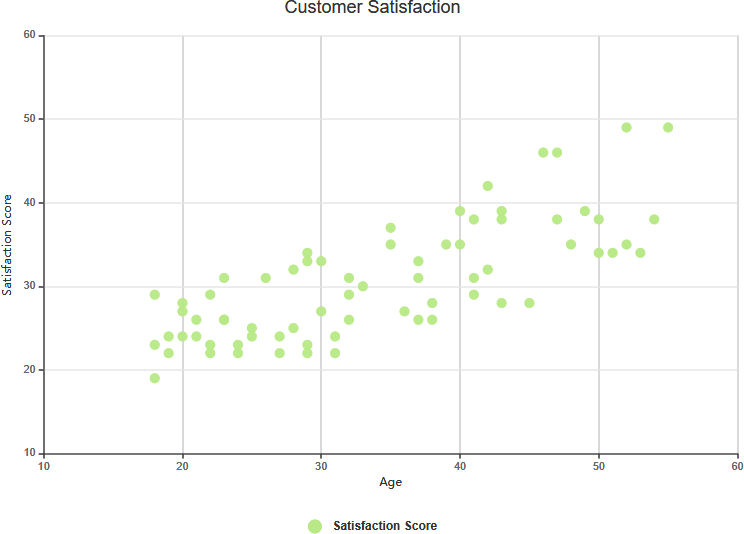
Złożona korelacja

Edytuj ten diagram

Brak korelacji

Edytuj ten diagram

Przykład wykresu rozproszenia: Długość ramienia w stosunku do klasy 11

Wykres rozproszenia powyżej ilustruje dane dotyczące wzrostu i długości ramion ośmiu uczniów klasy 11. Analizując zależność między wzrostem ucznia a długością ramienia, możemy zauważyć pewien trend. Ten trend pozwala oszacować długość ramienia ucznia na podstawie jego wzrostu, a także odwrotnie. W tym konkretnym wykresie widoczna jest dodatnia korelacja między długością ramienia a wzrostem.

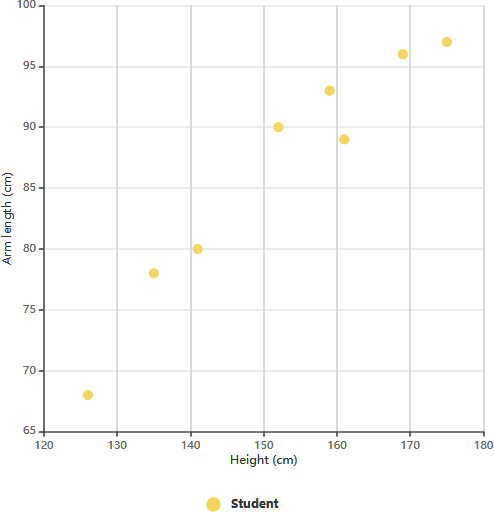
Po ustaleniu korelacji między tymi zmiennymi możemy przewidywać zachowanie zmiennej zależnej na podstawie pomiarów zmiennej niezależnej. Ten wykres okazuje się szczególnie wartościowy, gdy jedna zmienna jest łatwa do pomiaru, a druga nie. Na przykład, jeśli uczeń klasy 11 ma wzrost 148 cm, możemy oszacować, że jego długość ramienia wynosi około 84 cm.

Wnioski

W tym wykresie rozproszenia omówiliśmy podstawy wykresów rozproszenia oraz ich kluczową rolę w wizualizacji i analizie danych. Wykresy rozproszenia oferują potężne narzędzie do przedstawiania zależności między zmiennymi i odkrywania wzorców w danych. Przypomnijmy sobie kilka kluczowych wniosków z tego poradnika:

1. Definicja wykresów rozproszenia:Wykresy rozproszenia, znane również jako wykresy rozproszenia lub wykresy punktowe, przedstawiają punkty danych na płaszczyźnie dwuwymiarowej, przy czym każdy punkt reprezentuje unikalne obserwacje lub parę danych.
2. Zmienne i osie:Wykresy rozproszenia zwykle składają się z dwóch osi: osi X i osi Y. Te osie reprezentują zmienne badane, co pozwala wizualizować, jak zmiany jednej zmiennej są związane z zmianami drugiej.
3. Wzorce korelacji:Wykresy rozproszenia pomagają nam identyfikować różne wzorce korelacji między zmiennymi. Te wzorce można podzielić na silną korelację dodatnią, silną korelację ujemną, słabą korelację dodatnią, słabą korelację ujemną, złożoną korelację lub brak korelacji.
4. Przykłady z życia:W trakcie poradnika przedstawiliśmy przykłady z życia, aby ilustrować każdy z tych wzorców korelacji. Od badania wzrostu uczniów i długości ramion po analizę związku między liczbą godzin nauki a wynikami egzaminów, zobaczyliśmy, jak wykresy rozproszenia mogą być stosowane w różnych dziedzinach.
5. Moc prognozowania:Wykresy rozproszenia pozwalają nam przewidywać jedną zmienną na podstawie drugiej, dostarczając cennych informacji do podejmowania decyzji i zrozumienia relacji przyczynowo-skutkowych.
6. Złożone dane:Wykresy rozproszenia to elastyczne narzędzia, które mogą obsługiwać złożone dane, w tym sytuacje, w których relacja między zmiennymi nie jest prosta.
7. Interpretacja danych:Umiejętność interpretowania wykresów rozproszenia jest kluczowa dla badaczy, analityków i wszystkich tych, którzy chcą wyciągać istotne wnioski z danych.
8. Zastosowania praktyczne:Wykresy rozproszenia znajdują zastosowanie w dziedzinach takich jak ekonomia, nauki społeczne, nauki przyrodnicze, inżynieria i wiele innych. Pomagają one w identyfikowaniu trendów, korelacji i wartości odstających w zbiorach danych.

Opanowując sztukę tworzenia, analizowania i interpretowania wykresów rozproszenia, wyposażywszy się w cenną umiejętność wspomagania decyzji opartych na danych. Niezależnie od tego, czy jesteś uczniem, badaczem czy specjalistą, wykresy rozproszenia są wartościowym narzędziem w Twoim zestawie narzędzi analizy danych, oferując wgląd, który może prowadzić do świadomych decyzji i głębszego zrozumienia w wybranej dziedzinie.