Um Tutorial sobre Gráficos de Dispersão: Um Guia Rápido

Introdução

No campo da análise e visualização de dados, os gráficos de dispersão servem como ferramentas inestimáveis para descobrir relações entre variáveis. No nosso caso específico, geramos um gráfico de dispersão que explora a conexão intrigante entre o comprimento do braço e a altura entre um grupo de alunos do 11º ano. Essa representação visual de dados, composta por oito pontos de dados individuais, permite que investiguemos as dinâmicas entre essas duas características. Ao estudar os padrões dentro do gráfico de dispersão, podemos começar a fazer previsões sobre o comprimento do braço com base na altura e sobre a altura com base no comprimento do braço. Essa análise não apenas esclarece as características físicas desses alunos, mas também demonstra o poder dos gráficos de dispersão em revelar correlações.

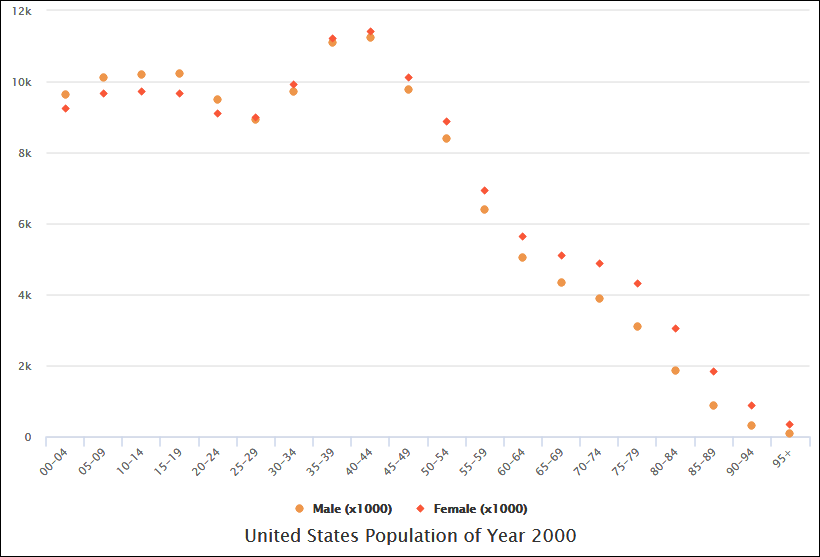
O que é um Gráfico de Dispersão

Um gráfico de dispersão, também conhecido como gráfico de dispersão ou gráfico de pontos, é um tipo de visualização de dados usado para exibir a relação entre duas variáveis. Cada ponto no gráfico representa um único ponto de dados, e a posição do ponto é determinada pelos valores das duas variáveis. Os gráficos de dispersão são úteis para identificar padrões, tendências e correlações nos dados. A seguir, darei uma explicação abrangente sobre gráficos de dispersão e exemplos para ilustrar seu uso.

Componentes de um Gráfico de Dispersão:

1. Eixo X: O eixo horizontal representa uma das variáveis sendo analisadas.
2. Eixo Y: O eixo vertical representa a outra variável sendo analisada.
3. Pontos de Dados: Cada ponto de dados no gráfico representa uma única observação ou par de dados, com um valor para a variável do eixo X e outro para a variável do eixo Y.
4. Título: Um título no topo do gráfico fornece contexto e informações sobre o que o gráfico representa.
5. Rótulos dos Eixos: Rótulos nos eixos X e Y fornecem informações sobre as unidades ou categorias das variáveis.
6. Legenda: Se múltiplos conjuntos de dados forem exibidos no mesmo gráfico, uma legenda pode ser usada para diferenciá-los.

Exemplos de Gráficos de Dispersão:

1. Correlação Positiva Forte:
   • Definição: O valor de Y aumenta à medida que o valor de X aumenta.
   • Exemplo: Em um estudo sobre o número de horas gastos estudando e as notas em provas, à medida que o número de horas gastos estudando (X) aumenta, as notas em provas (Y) também aumentam. Isso indica uma forte correlação positiva.
2. Correlação Negativa Forte:
   • Definição: O valor de Y diminui à medida que o valor de X aumenta.
   • Exemplo:Em um estudo sobre a quantidade de chuva e o número de horas que as pessoas passam ao ar livre, à medida que a quantidade de chuva (X) aumenta, o número de horas passadas ao ar livre (Y) diminui. Isso demonstra uma forte correlação negativa.
3. Correlação Positiva Fraca:
   • Definição:O valor de Y aumenta ligeiramente à medida que o valor de X aumenta.
   • Exemplo:Analisando a idade das pessoas e sua renda anual, você pode perceber que, à medida que a idade (X) aumenta, a renda (Y) aumenta ligeiramente. Isso indica uma correlação positiva fraca.
4. Correlação Negativa Fraca:
   • Definição:O valor de Y diminui ligeiramente à medida que o valor de X aumenta.
   • Exemplo:Estudando o tempo gasto no deslocamento para o trabalho e os níveis de energia, você pode perceber que, à medida que o tempo de deslocamento (X) aumenta ligeiramente, os níveis de energia (Y) diminuem ligeiramente. Isso sugere uma correlação negativa fraca.
5. Correlação Complexa:
   • Definição:O valor de Y parece estar relacionado ao valor de X, mas a relação não é facilmente determinada.
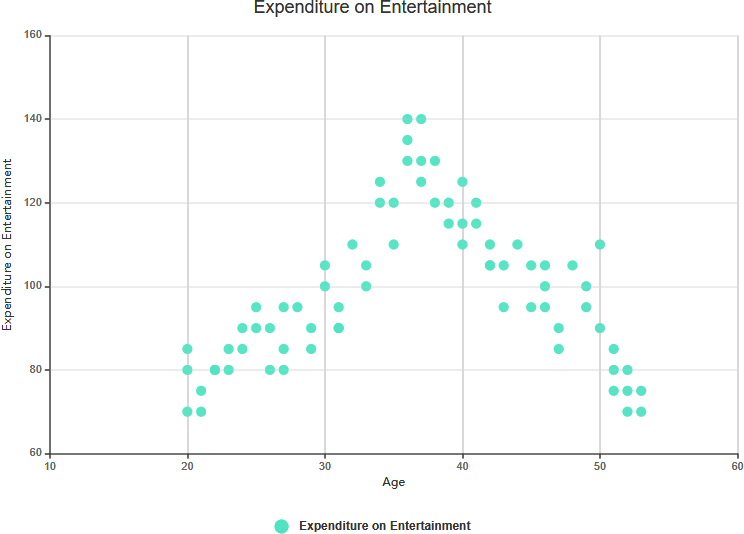
   • Exemplo:Em uma análise do gasto com publicidade e vendas de produtos, a relação entre os dois pode parecer complexa, com flutuações e sem uma direção clara.
6. Sem Correlação:
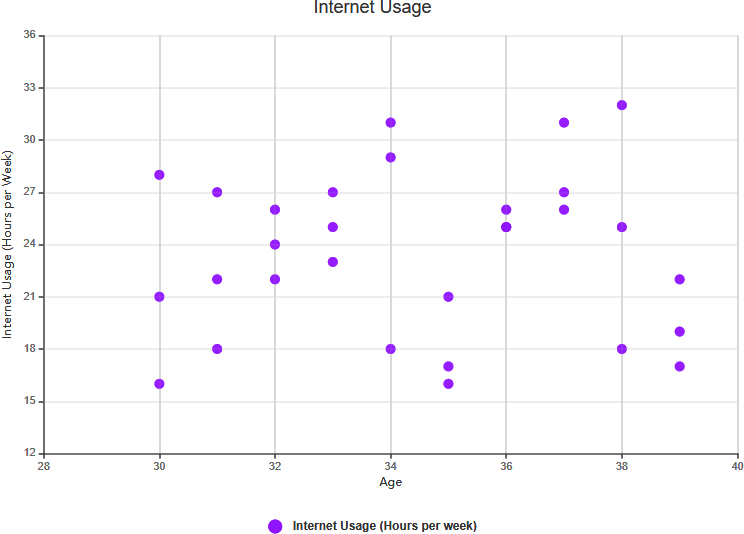
   • Definição:Não há uma conexão demonstrada entre as duas variáveis.
   • Exemplo:Se você analisar o tamanho do sapato e os escores de QI, pode perceber que não há uma relação significativa entre eles. Neste caso, não há correlação.

Compreender esses padrões de correlação é essencial para interpretar gráficos de dispersão e tirar conclusões significativas dos dados. A análise de correlação ajuda na realização de previsões, na compreensão das relações de causa e efeito e na identificação de tendências em diversos campos, como economia, ciências sociais e ciências naturais.

Correlação Positiva Forte

Editar este Diagrama

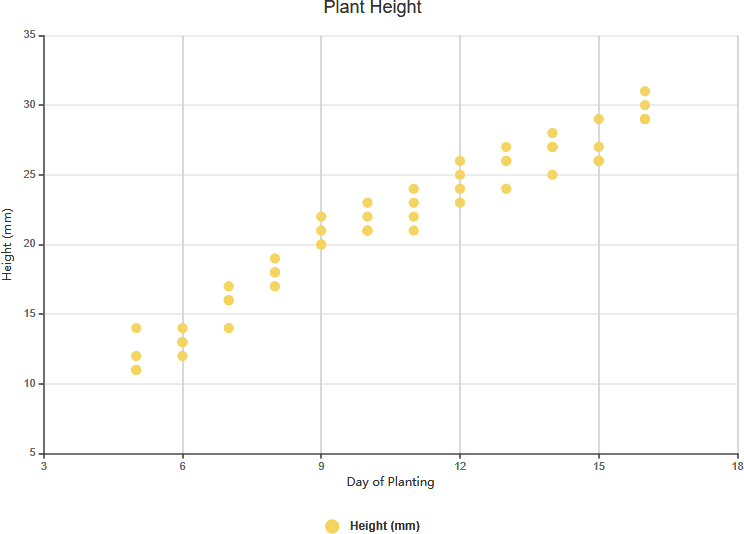
Correlação Negativa Forte

Editar este Diagrama

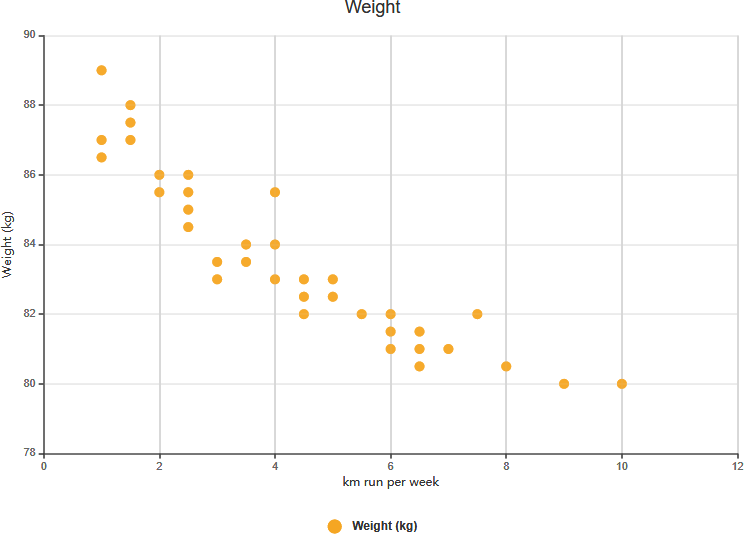
Correlação Positiva Fraca

Editar este Diagrama

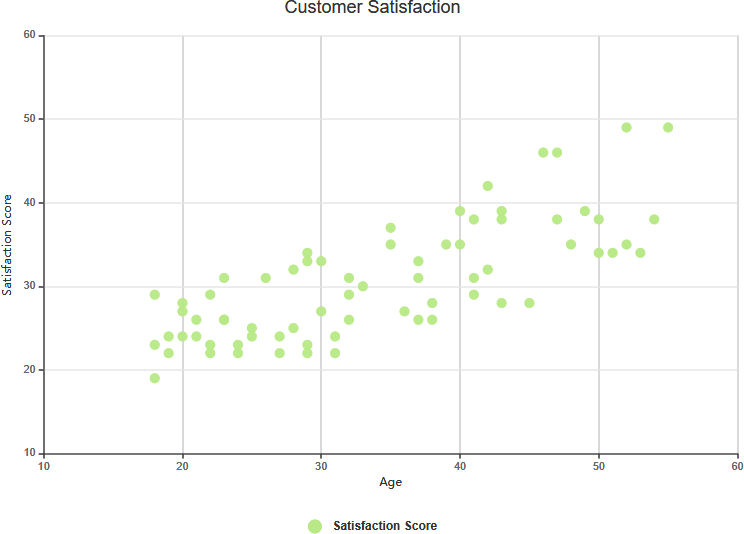
Correlação Complexa

Edite este Diagrama

Sem Correlação

Edite este Diagrama

Exemplo de Gráfico de Dispersão: Comprimento do Braço vs. 11º Ano

O gráfico de dispersão acima ilustra dados sobre a altura e o comprimento do braço de oito alunos do 11º ano. Ao examinar a relação entre a altura de um aluno e o comprimento do braço, podemos identificar uma tendência. Essa tendência permite estimar o comprimento do braço de um aluno com base na sua altura fornecida, e vice-versa. Neste gráfico específico, é evidente uma correlação positiva entre o comprimento do braço e a altura.

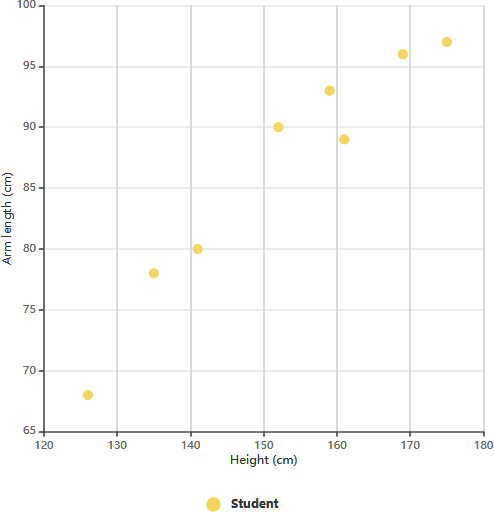
Após estabelecer a correlação entre essas variáveis, podemos fazer previsões sobre o comportamento da variável dependente usando as medições da variável independente. Este gráfico prova particularmente valioso quando uma das variáveis é fácil de medir, enquanto a outra não o é. Por exemplo, se um aluno do 11º ano tem uma altura de 148 cm, podemos estimar que seu comprimento do braço é aproximadamente 84 cm.

Conclusão

Neste gráfico de dispersão, exploramos os fundamentos dos gráficos de dispersão e sua função essencial na visualização e análise de dados. Os gráficos de dispersão fornecem uma forma poderosa de representar relações entre variáveis e descobrir padrões nos dados. Vamos recapitular algumas conclusões-chave deste tutorial:

1. Definição de Gráficos de Dispersão:Gráficos de dispersão, também conhecidos como gráficos de dispersão ou gráficos de pontos, exibem pontos de dados em um plano bidimensional, com cada ponto representando uma observação única ou um par de dados.
2. Variáveis e Eixos:Os gráficos de dispersão geralmente consistem em dois eixos: o eixo X e o eixo Y. Esses eixos representam as variáveis em estudo, possibilitando visualizar como as mudanças em uma variável se relacionam com as mudanças em outra.
3. Padrões de Correlação:Os gráficos de dispersão nos ajudam a identificar diferentes padrões de correlação entre variáveis. Esses padrões podem ser categorizados como correlação positiva forte, correlação negativa forte, correlação positiva fraca, correlação negativa fraca, correlação complexa ou sem correlação.
4. Exemplos do Mundo Real:Ao longo do tutorial, fornecemos exemplos do mundo real para ilustrar cada um desses padrões de correlação. Desde o estudo da altura e do comprimento do braço de alunos até a análise da relação entre horas de estudo e notas em provas, vimos como os gráficos de dispersão podem ser aplicados em diversos domínios.
5. Poder Preditivo:Os gráficos de dispersão permitem que façamos previsões sobre uma variável com base na outra, fornecendo insights valiosos para a tomada de decisões e para a compreensão de relações causais.
6. Dados Complexos:Os gráficos de dispersão são ferramentas versáteis que podem lidar com dados complexos, incluindo situações em que a relação entre as variáveis não é direta.
7. Interpretação de Dados:A capacidade de interpretar gráficos de dispersão é crucial para pesquisadores, analistas e qualquer pessoa que busque tirar conclusões significativas dos dados.
8. Aplicações Práticas:Os gráficos de dispersão têm aplicações em áreas tão diversas quanto economia, ciências sociais, ciências naturais, engenharia e muitas outras. Eles ajudam a identificar tendências, correlações e valores atípicos dentro de conjuntos de dados.

Ao dominar a arte de criar, analisar e interpretar gráficos de dispersão, você se equipa com uma habilidade valiosa para a tomada de decisões baseada em dados. Seja você um estudante, um pesquisador ou um profissional, os gráficos de dispersão são uma ferramenta valiosa na sua caixa de ferramentas de análise de dados, oferecendo insights que podem impulsionar escolhas informadas e uma compreensão mais profunda em sua área escolhida.