Учебное пособие по диаграмме рассеяния: Краткое руководство

Введение

В области анализа и визуализации данных диаграммы рассеяния служат бесценными инструментами для выявления взаимосвязей между переменными. В нашем конкретном случае мы создали диаграмму рассеяния, которая исследует интересную связь между длиной руки и ростом среди группы учеников 11 класса. Это визуальное представление данных, состоящее из восьми отдельных точек данных, позволяет нам глубоко изучить динамику между этими двумя характеристиками. Изучая паттерны на диаграмме рассеяния, мы можем начать делать прогнозы о длине руки на основе роста и наоборот. Этот анализ не только раскрывает особенности физического развития этих учеников, но и демонстрирует мощь диаграмм рассеяния в выявлении корреляций.

Что такое диаграмма рассеяния

Диаграмма рассеяниядиаграмма рассеяния, также известная как диаграмма рассеяния или точечный график, представляет собой тип визуализации данных, используемый для отображения взаимосвязи между двумя переменными. Каждая точка на графике представляет собой отдельную точку данных, а её положение определяется значениями двух переменных. Диаграммы рассеяния полезны для выявления паттернов, тенденций и корреляций в данных. Ниже я предоставлю подробное объяснение диаграмм рассеяния и примеры, иллюстрирующие их применение.

Компоненты диаграммы рассеяния:

1. Ось X: Горизонтальная ось представляет одну из анализируемых переменных.
2. Ось Y: Вертикальная ось представляет другую анализируемую переменную.
3. Точки данных: Каждая точка на графике представляет собой отдельное наблюдение или пару данных, с одним значением для переменной на оси X и другим — для переменной на оси Y.
4. Заголовок: Заголовок в верхней части графика предоставляет контекст и информацию о том, что представляет собой график.
5. Метки осей: Метки на оси X и оси Y предоставляют информацию о единицах измерения или категориях переменных.
6. Легенда: Если на одном графике отображается несколько наборов данных, легенда может использоваться для их различения.

Примеры диаграмм рассеяния:

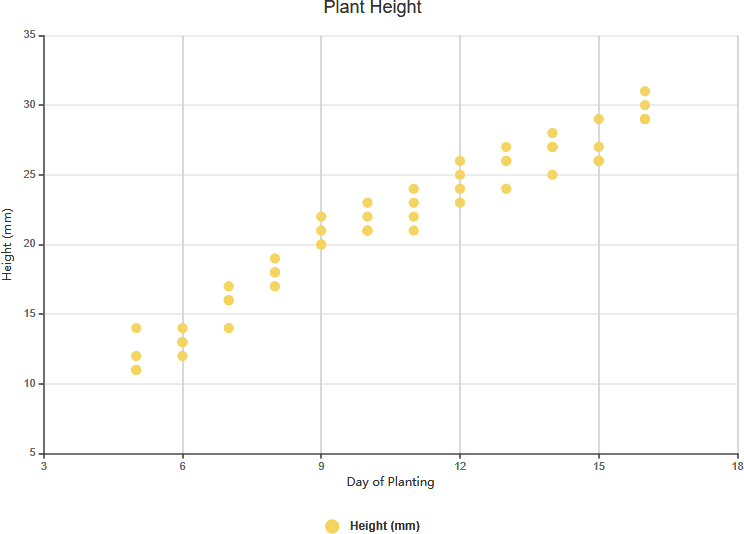
1. Сильная положительная корреляция:
   • Определение: Значение Y увеличивается по мере увеличения значения X.
   • Пример: В исследовании количества часов, потраченных на учёбу, и оценок на экзаменах, по мере увеличения количества часов, потраченных на учёбу (X), оценки на экзаменах (Y) также увеличиваются. Это указывает на сильную положительную корреляцию.
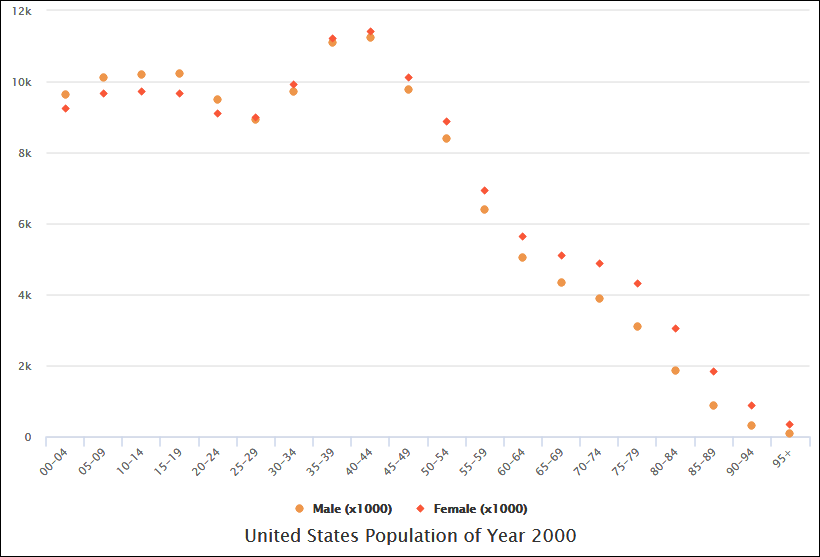
2. Сильная отрицательная корреляция:
   • Определение: Значение Y уменьшается по мере увеличения значения X.
   • Пример:В исследовании количества осадков и количества часов, которые люди проводят на открытом воздухе, по мере увеличения количества осадков (X) количество часов, проведенных на открытом воздухе (Y), уменьшается. Это демонстрирует сильную отрицательную корреляцию.
3. Слабая положительная корреляция:
   • Определение:Значение Y незначительно увеличивается по мере увеличения значения X.
   • Пример:Анализируя возраст людей и их годовой доход, вы можете обнаружить, что по мере увеличения возраста (X) доход (Y) незначительно возрастает. Это указывает на слабую положительную корреляцию.
4. Слабая отрицательная корреляция:
   • Определение:Значение Y незначительно уменьшается по мере увеличения значения X.
   • Пример:Изучая количество времени, затрачиваемое на поездку на работу, и уровень энергии, вы можете заметить, что по мере незначительного увеличения времени поездки (X) уровень энергии (Y) незначительно снижается. Это указывает на слабую отрицательную корреляцию.
5. Сложная корреляция:
   • Определение:Значение Y, похоже, связано со значением X, но связь трудно определить.
   • Пример:В анализе расходов на рекламу и объема продаж продукта связь между ними может показаться сложной, с колебаниями и отсутствием четкого направления.
6. Отсутствие корреляции:
   • Определение:Между двумя переменными нет доказанной связи.
   • Пример:Если вы изучите размер обуви и показатели IQ, вы можете обнаружить, что между ними нет значимой связи. В этом случае отсутствует корреляция.

Понимание этих паттернов корреляции необходимо для интерпретации диаграмм рассеяния и извлечения осмысленных выводов из данных. Анализ корреляции помогает делать прогнозы, понимать причинно-следственные связи и выявлять тенденции в различных областях, таких как экономика, социальные науки и естественные науки.

Сильная положительная корреляция

Редактировать эту диаграмму

Сильная отрицательная корреляция

Редактировать эту диаграмму

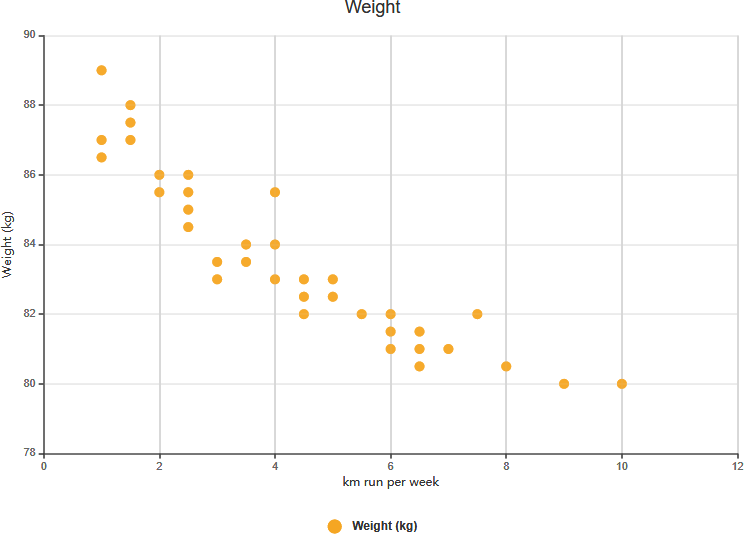
Слабая положительная корреляция

Редактировать эту диаграмму

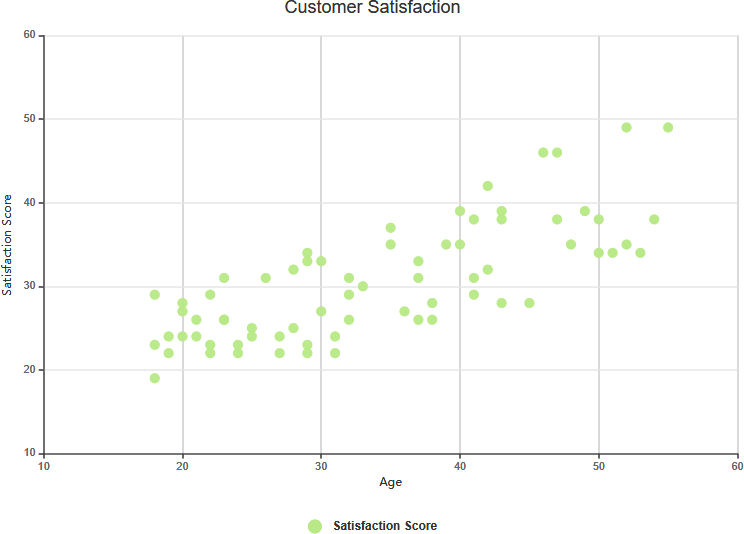
Сложная корреляция

Редактировать эту диаграмму

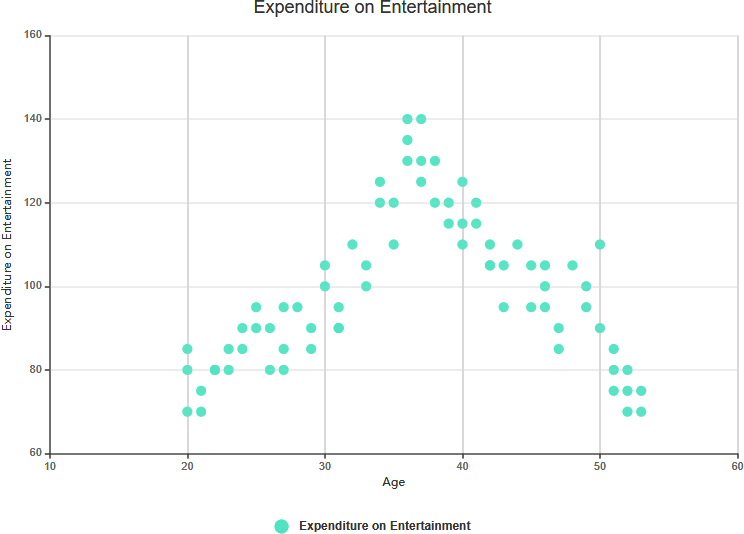
Нет корреляции

Редактировать эту диаграмму

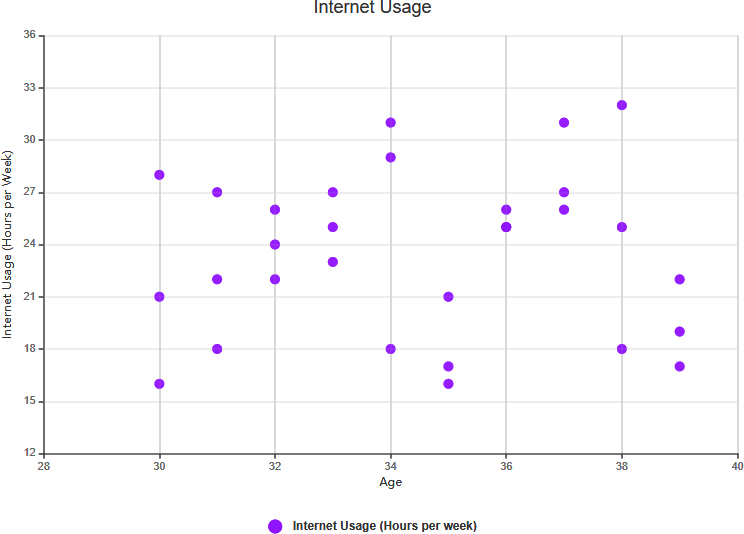
Пример диаграммы рассеяния: длина руки по сравнению с 11 классом

Диаграмма рассеяния выше иллюстрирует данные о росте и длине руки восьми учеников 11 класса. Изучая связь между ростом и длиной руки ученика, мы можем выявить тенденцию. Эта тенденция позволяет оценить длину руки ученика на основе его роста и наоборот. В этой диаграмме очевидна положительная корреляция между длиной руки и ростом.

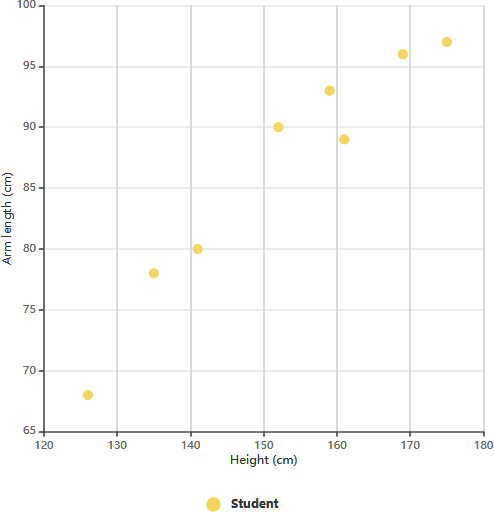
После установления корреляции между этими переменными мы можем делать прогнозы о поведении зависимой переменной, используя измерения независимой переменной. Эта диаграмма особенно полезна, когда одна из переменных легко измерима, а другая — нет. Например, если ученик 11 класса имеет рост 148 см, мы можем оценить, что его длина руки составляет примерно 84 см.

Заключение

В этой диаграмме рассеяния мы изучили основы диаграмм рассеяния и их важную роль в визуализации и анализе данных. Диаграммы рассеяния предоставляют мощный способ отображения взаимосвязей между переменными и выявления паттернов в данных. Давайте повторим некоторые ключевые выводы из этого учебного пособия:

1. Определение диаграмм рассеяния:Диаграммы рассеяния, также известные как диаграммы рассеяния или графики рассеяния, отображают точки данных на двумерной плоскости, при этом каждая точка представляет собой уникальное наблюдение или пару данных.
2. Переменные и оси:Диаграммы рассеяния обычно состоят из двух осей: оси X и оси Y. Эти оси представляют изучаемые переменные, что позволяет визуализировать, как изменения одной переменной связаны с изменениями другой.
3. Паттерны корреляции:Диаграммы рассеяния помогают нам выявлять различные паттерны корреляции между переменными. Эти паттерны можно классифицировать как сильная положительная корреляция, сильная отрицательная корреляция, слабая положительная корреляция, слабая отрицательная корреляция, сложная корреляция или отсутствие корреляции.
4. Реальные примеры:На протяжении всего учебного пособия мы привели реальные примеры, чтобы проиллюстрировать каждый из этих паттернов корреляции. От изучения роста и длины руки учеников до анализа связи между количеством часов учебы и результатами экзаменов мы увидели, как диаграммы рассеяния могут применяться в различных областях.
5. Предиктивная сила:Диаграммы рассеяния позволяют делать прогнозы о одной переменной на основе другой, обеспечивая ценные сведения для принятия решений и понимания причинно-следственных связей.
6. Сложные данные:Диаграммы рассеяния — универсальные инструменты, способные обрабатывать сложные данные, включая ситуации, когда связь между переменными не является прямолинейной.
7. Интерпретация данных:Умение интерпретировать диаграммы рассеяния имеет решающее значение для исследователей, аналитиков и всех, кто стремится сделать осмысленные выводы из данных.
8. Практическое применение:Диаграммы рассеяния находят применение в самых разных областях, таких как экономика, социальные науки, естественные науки, инженерия и др. Они помогают выявлять тенденции, корреляции и выбросы в наборах данных.

Овладев искусством создания, анализа и интерпретации диаграмм рассеяния, вы оснащаете себя ценным навыком для принятия решений на основе данных. Независимо от того, являетесь ли вы студентом, исследователем или профессионалом, диаграммы рассеяния являются ценным инструментом в вашем арсенале анализа данных, предоставляя глубокие инсайты, которые способны направлять обоснованные решения и углублять понимание в вашей области.