散布図のチュートリアル：簡単なガイド

はじめに

データ分析と可視化の分野において、散布図は変数間の関係を明らかにするための貴重なツールです。今回のケースでは、11年生の一群の生徒における腕の長さと身長の興味深い関係を調査するための散布図を作成しました。8つの個別のデータポイントから構成されるこのデータの視覚的表現により、これらの2つの属性間の関係を深く探求できます。散布図内のパターンを分析することで、身長から腕の長さを予測したり、腕の長さから身長を予測したりすることができるようになります。この分析は、これらの生徒の身体的特徴についての理解を深めるだけでなく、散布図が相関関係を明確にする力を持っていることを示しています。

散布図とは何か

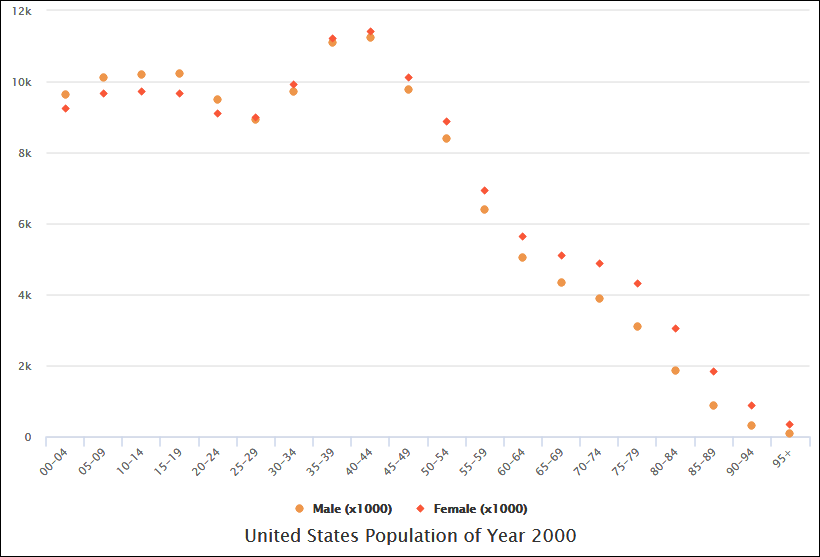
一種の散布図、別名散布図または散布グラフとも呼ばれる、2つの変数間の関係を表示するために用いられるデータ可視化の一種です。図上の各点は1つのデータポイントを表しており、その位置は2つの変数の値によって決定されます。散布図はデータ内のパターン、トレンド、相関関係を特定するのに役立ちます。以下では、散布図の包括的な説明とその使用例を示します。

散布図の構成要素：

1. X軸：水平軸は分析対象の変数のうちの1つを表します。
2. Y軸：垂直軸は分析対象のもう1つの変数を表します。
3. データポイント：図上の各データポイントは、x軸の変数とy軸の変数それぞれに対応する1つの観測値またはデータペアを表します。
4. タイトル：図の上部にあるタイトルは、図が何を表しているかに関する文脈と情報を提供します。
5. 軸ラベル：x軸およびy軸のラベルは、変数の単位やカテゴリに関する情報を提供します。
6. 凡例：複数のデータセットが同じ図に表示される場合、凡例を用いてそれらを区別することができます。

散布図の例：

1. 強い正の相関：
   • 定義：Xの値が増加するにつれて、Yの値も増加する。
   • 例：勉強時間と試験成績の関係を調査する研究において、勉強時間（X）が増加するにつれて、試験成績（Y）も増加します。これは強い正の相関を示しています。
2. 強い負の相関：
   • 定義：Xの値が増加するにつれて、Yの値は減少する。
   • 例：降雨量と屋外に過ごす時間の長さに関する研究において、降雨量（X）が増加するにつれて、屋外に過ごす時間（Y）は減少する。これは強い負の相関を示している。
3. 弱い正の相関：
   • 定義：Xの値が増加するにつれて、Yの値はわずかに増加する。
   • 例：個人の年齢と年間収入を分析すると、年齢（X）が増加するにつれて収入（Y）がわずかに増加することがある。これは弱い正の相関を示している。
4. 弱い負の相関：
   • 定義：Xの値が増加するにつれて、Yの値はわずかに減少する。
   • 例：通勤時間とエネルギーのレベルを調査すると、通勤時間（X）がわずかに増加するにつれてエネルギーのレベル（Y）もわずかに低下することがある。これは弱い負の相関を示唆している。
5. 複雑な相関：
   • 定義：Yの値はXの値に関連しているように見えるが、その関係は容易に特定できない。
   • 例：広告費と製品販売数の分析において、両者の関係は複雑に見え、変動があり、明確な方向性がない場合がある。
6. 相関なし：
   • 定義：二つの変数の間に明確な関連性は示されていない。
   • 例：靴のサイズと知能指数（IQ）を調べると、それらの間に有意な関係がないことがわかる場合がある。この場合、相関はない。

これらの相関パターンを理解することは、散布図の解釈やデータから意味のある結論を導くために不可欠である。相関分析は予測の立案、因果関係の理解、経済学、社会科学、自然科学などさまざまな分野におけるトレンドの特定に役立つ。

強い正の相関

この図を編集する

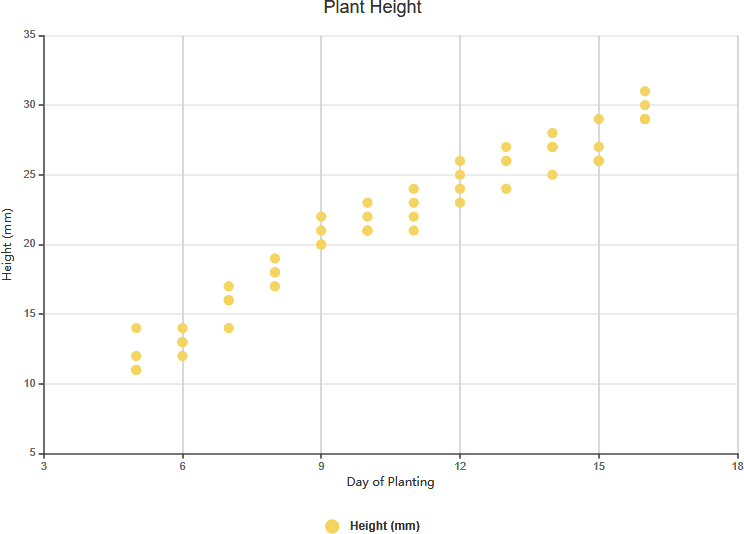
強い負の相関

この図を編集する

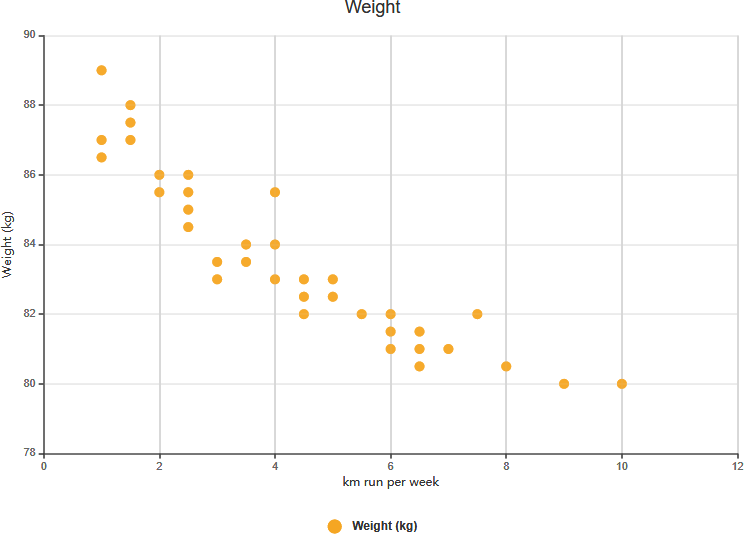
弱い正の相関

この図を編集する

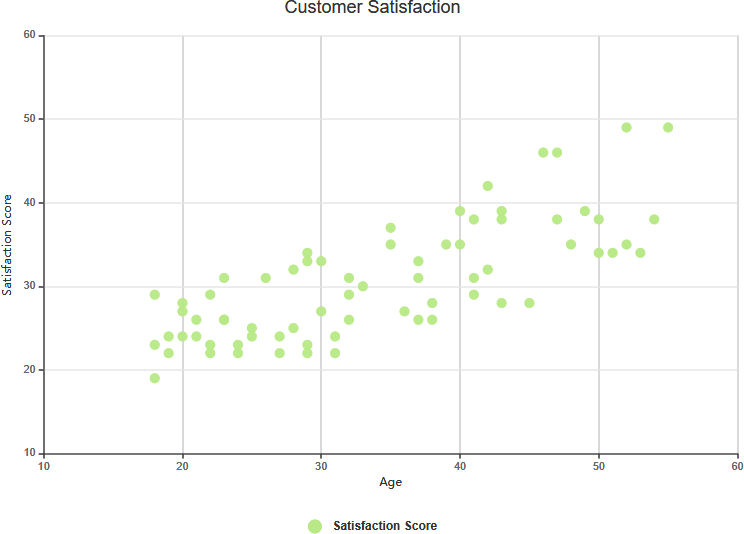
複雑な相関

この図を編集する

相関なし

この図を編集する

散布図の例：腕の長さ vs. 11年生

上記の散布図は、8人の11年生の身長と腕の長さに関するデータを示しています。生徒の身長と腕の長さの関係を検討することで、トレンドを把握できます。このトレンドにより、身長から腕の長さを推定したり、逆に腕の長さから身長を推定したりできます。この特定の図では、腕の長さと身長の間に正の相関があることが明らかです。

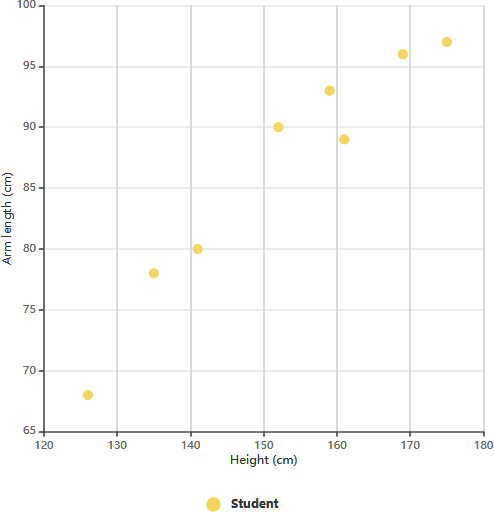
これらの変数間の相関関係を確認した後、独立変数の測定値を使って従属変数の挙動を予測できます。特に一方の変数は簡単に測定できるが、もう一方は難しい場合に、この図は特に有用です。たとえば、11年生の生徒の身長が148cmの場合、腕の長さは約84cmであると推定できます。

結論

この散布図において、散布図の基本的な性質とデータ可視化および分析におけるその重要な役割について学びました。散布図は変数間の関係を示し、データ内のパターンを明らかにする強力な手段です。このチュートリアルの主なポイントを振り返りましょう：

1. 散布図の定義：散布図は、散布図または散布グラフとも呼ばれるもので、2次元平面上にデータポイントを表示し、各ポイントは一意の観測値またはデータペアを表します。
2. 変数と軸：散布図は通常、X軸とY軸の2つの軸から構成されています。これらの軸は研究中の変数を表し、一方の変数の変化が他方の変数の変化とどのように関連しているかを視覚化できるようにします。
3. 相関パターン：散布図は、変数間の異なる相関パターンを特定するのに役立ちます。これらのパターンは、強い正の相関、強い負の相関、弱い正の相関、弱い負の相関、複雑な相関、または相関なしのいずれかに分類できます。
4. 実際の例：このチュートリアルを通じて、これらの相関パターンを説明するために実際の例を提示しました。生徒の身長と腕の長さを研究したり、勉強時間と試験成績の関係を分析したりすることで、散布図がさまざまな分野に応用できることを確認しました。
5. 予測力：散布図により、一方の変数に基づいて他方の変数について予測が可能となり、意思決定や因果関係の理解に役立つ貴重な洞察を提供します。
6. 複雑なデータ：散布図は、変数間の関係が明確でない場合を含む、複雑なデータを扱える汎用的なツールです。
7. データの解釈：散布図を解釈する能力は、研究者や分析者、そしてデータから意味のある結論を導きたいすべての人にとって重要です。
8. 実用的応用：散布図は経済学、社会科学、自然科学、工学など多様な分野で応用されています。データセット内のトレンド、相関関係、外れ値の特定に役立ちます。

散布図の作成、分析、解釈の技術を習得することで、データ駆動型の意思決定に役立つ貴重なスキルを身につけます。学生であろうと研究者であろうとプロフェッショナルであろうと、散布図はデータ分析のツールキットにおいて重要な役割を果たし、選択した分野における情報に基づいた意思決定やより深い理解を促進する洞察を提供します。