Hướng dẫn về biểu đồ phân tán: Hướng dẫn nhanh
Giới thiệu
Trong lĩnh vực phân tích và trực quan hóa dữ liệu, biểu đồ phân tán đóng vai trò là công cụ quý giá để phát hiện mối quan hệ giữa các biến số. Trong trường hợp cụ thể này, chúng tôi đã tạo ra một biểu đồ phân tán để khám phá mối liên hệ thú vị giữa chiều dài cánh tay và chiều cao ở một nhóm học sinh lớp 11. Biểu đồ trực quan này, gồm tám điểm dữ liệu riêng lẻ, giúp chúng ta nghiên cứu sâu hơn về mối quan hệ giữa hai đặc trưng này. Bằng cách phân tích các mẫu trong biểu đồ phân tán, chúng ta có thể bắt đầu đưa ra dự đoán về chiều dài cánh tay dựa trên chiều cao và ngược lại. Phân tích này không chỉ làm sáng tỏ các đặc điểm thể chất của các học sinh mà còn minh chứng cho sức mạnh của biểu đồ phân tán trong việc làm rõ các mối tương quan.
Biểu đồ phân tán là gì
Một biểu đồ phân tán, còn được gọi là biểu đồ phân tán hoặc đồ thị phân tán, là một dạng trực quan hóa dữ liệu dùng để hiển thị mối quan hệ giữa hai biến số. Mỗi điểm trên biểu đồ đại diện cho một điểm dữ liệu riêng lẻ, và vị trí của điểm này được xác định bởi giá trị của hai biến số. Biểu đồ phân tán hữu ích trong việc phát hiện các mẫu, xu hướng và mối tương quan trong dữ liệu. Dưới đây, tôi sẽ cung cấp một giải thích toàn diện về biểu đồ phân tán và các ví dụ minh họa cách sử dụng chúng.
Các thành phần của biểu đồ phân tán:
- Trục X:Trục ngang đại diện cho một trong các biến số đang được phân tích.
- Trục Y:Trục dọc đại diện cho biến số còn lại đang được phân tích.
- Các điểm dữ liệu:Mỗi điểm dữ liệu trên biểu đồ đại diện cho một quan sát hoặc cặp dữ liệu riêng lẻ, với một giá trị cho biến số trục X và một giá trị khác cho biến số trục Y.
- Tiêu đề:Tiêu đề ở đầu biểu đồ cung cấp bối cảnh và thông tin về nội dung biểu đồ đang thể hiện.
- Nhãn trục:Nhãn trên trục X và trục Y cung cấp thông tin về đơn vị hoặc loại dữ liệu của các biến số.
- Chú thích:Nếu nhiều bộ dữ liệu được hiển thị trên cùng một biểu đồ, chú thích có thể được sử dụng để phân biệt chúng.
Ví dụ về biểu đồ phân tán:
Biểu đồ phân tán thể hiện nhiều mẫu tương quan khác nhau, mỗi mẫu phản ánh mối liên hệ giữa các giá trị X và Y. Để minh họa các mẫu này, chúng ta hãy đưa ra ví dụ cho từng loại:
- Tương quan dương mạnh:
- Định nghĩa:Giá trị của Y tăng khi giá trị của X tăng.
- Ví dụ:Trong một nghiên cứu về số giờ dành để học và điểm số bài kiểm tra, khi số giờ học (X) tăng lên, điểm số bài kiểm tra (Y) cũng tăng theo. Điều này cho thấy mối tương quan dương mạnh.
- Tương quan âm mạnh:
- Định nghĩa:Giá trị của Y giảm khi giá trị của X tăng.
- Ví dụ:Trong một nghiên cứu về lượng mưa và số giờ con người dành ngoài trời, khi lượng mưa (X) tăng lên, số giờ dành ngoài trời (Y) giảm đi. Điều này cho thấy mối tương quan âm mạnh.
- Tương quan dương yếu:
- Định nghĩa:Giá trị của Y tăng nhẹ khi giá trị của X tăng lên.
- Ví dụ:Phân tích độ tuổi của các cá nhân và thu nhập hàng năm, bạn có thể thấy rằng khi độ tuổi (X) tăng lên, thu nhập (Y) tăng nhẹ. Điều này cho thấy mối tương quan dương yếu.
- Tương quan âm yếu:
- Định nghĩa:Giá trị của Y giảm nhẹ khi giá trị của X tăng lên.
- Ví dụ:Nghiên cứu thời gian di chuyển đến nơi làm việc và mức năng lượng, bạn có thể nhận thấy rằng khi thời gian di chuyển (X) tăng nhẹ, mức năng lượng (Y) giảm nhẹ. Điều này gợi ý mối tương quan âm yếu.
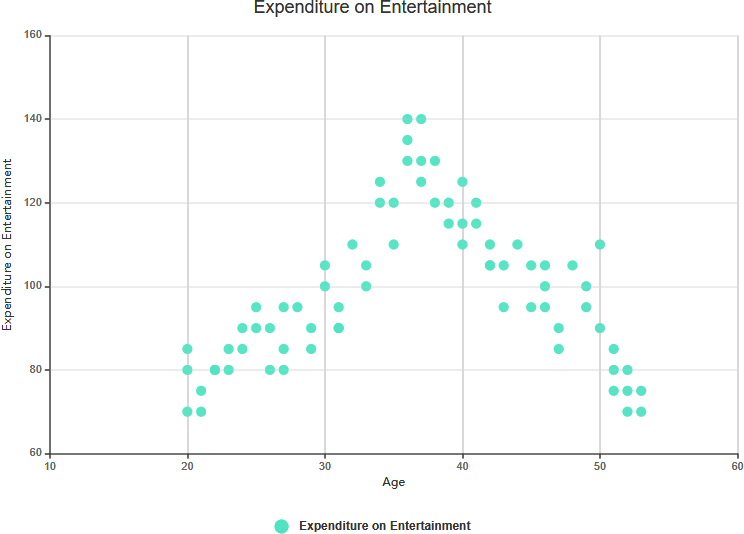
- Tương quan phức tạp:
- Định nghĩa:Giá trị của Y dường như liên quan đến giá trị của X, nhưng mối quan hệ này không dễ xác định.
- Ví dụ:Trong phân tích chi phí quảng cáo và doanh số sản phẩm, mối quan hệ giữa hai yếu tố này có thể trông phức tạp, với những biến động và không có hướng rõ ràng.
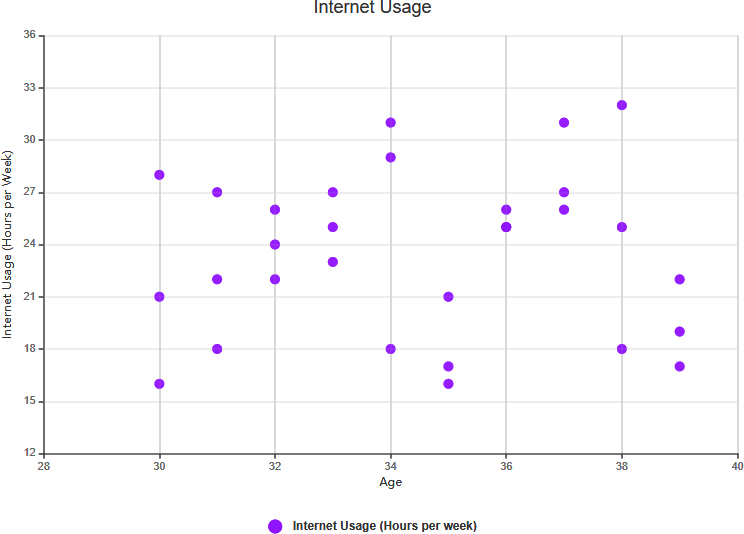
- Không có tương quan:
- Định nghĩa:Không có mối liên hệ được chứng minh giữa hai biến số.
- Ví dụ:Nếu bạn xem xét kích cỡ giày và điểm số IQ, bạn có thể thấy rằng không có mối quan hệ đáng kể giữa chúng. Trong trường hợp này, không có tương quan.
Hiểu rõ các mẫu tương quan này là điều cần thiết để diễn giải biểu đồ phân tán và rút ra những kết luận có ý nghĩa từ dữ liệu. Phân tích tương quan giúp đưa ra dự đoán, hiểu mối quan hệ nhân quả và phát hiện xu hướng trong nhiều lĩnh vực như kinh tế, khoa học xã hội và khoa học tự nhiên.
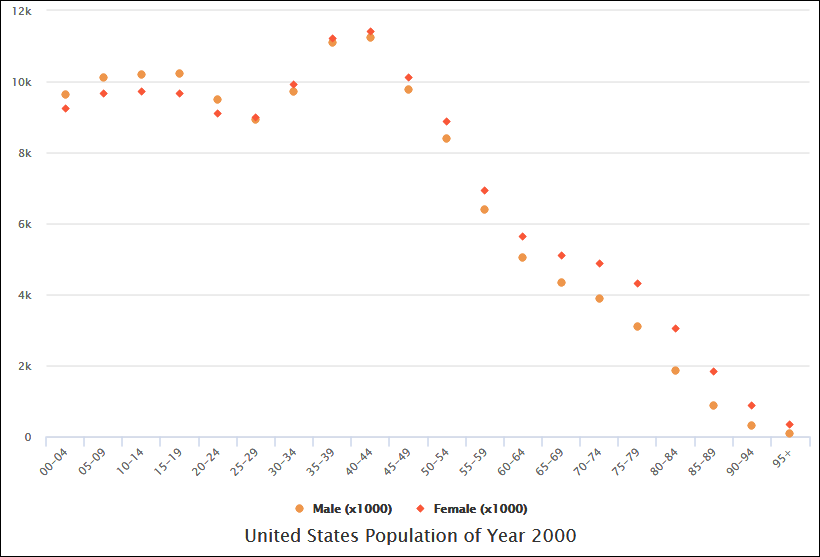
Tương quan dương mạnh
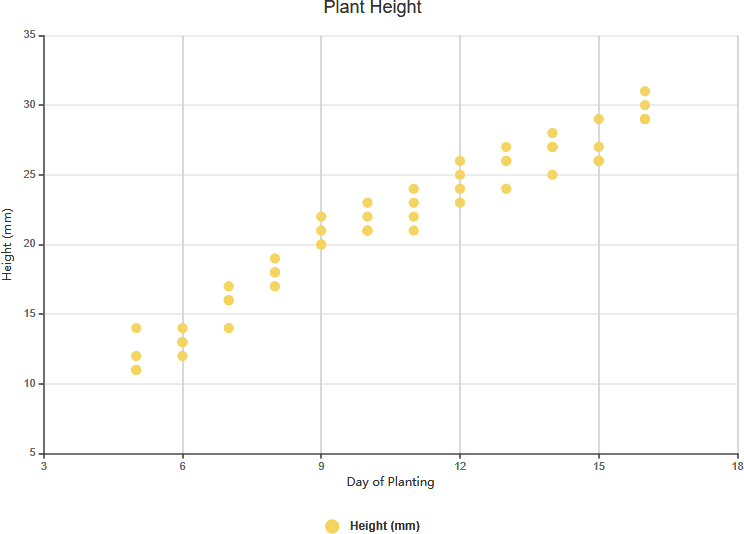
Tương quan âm mạnh
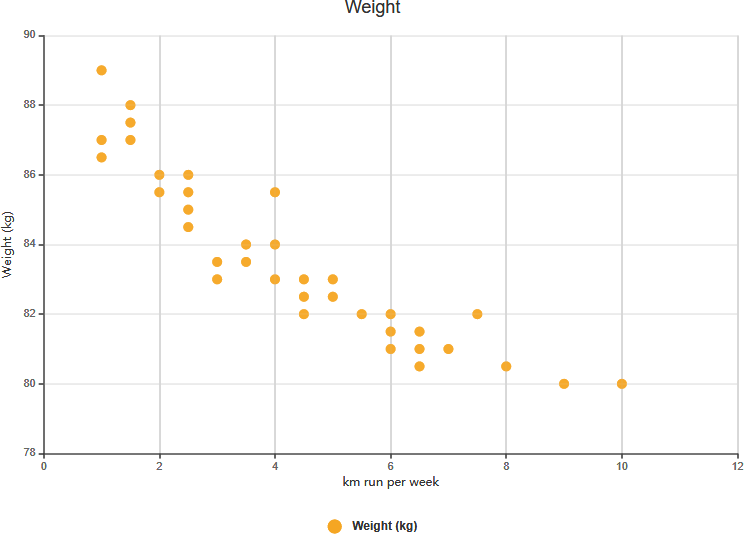
Tương quan dương yếu
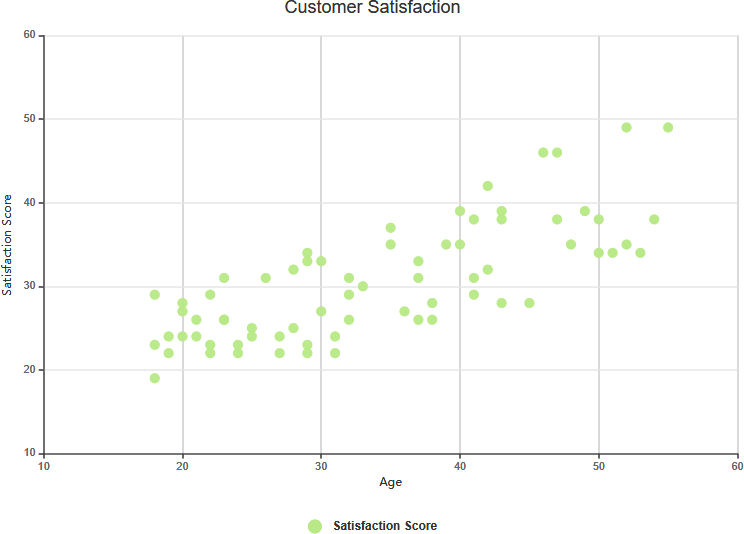
Tương quan phức tạp
Không có tương quan
Ví dụ biểu đồ phân tán: Chiều dài cánh tay so với lớp 11
Biểu đồ phân tán ở trên minh họa dữ liệu về chiều cao và chiều dài cánh tay của tám học sinh lớp 11. Bằng cách xem xét mối quan hệ giữa chiều cao và chiều dài cánh tay của một học sinh, chúng ta có thể nhận thấy một xu hướng. Xu hướng này cho phép chúng ta ước tính chiều dài cánh tay của một học sinh dựa trên chiều cao đã cho, và ngược lại. Trong biểu đồ này, rõ ràng là có mối tương quan dương giữa chiều dài cánh tay và chiều cao.
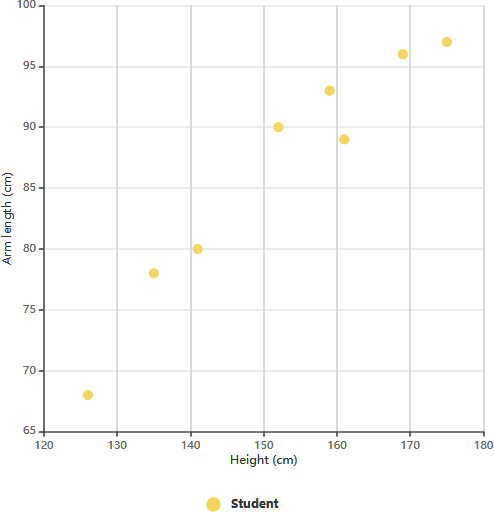
Sau khi xác lập mối tương quan giữa các biến này, chúng ta có thể đưa ra dự đoán về hành vi của biến phụ thuộc dựa trên các đo lường của biến độc lập. Biểu đồ này đặc biệt hữu ích khi một trong hai biến dễ đo lường hơn biến còn lại. Ví dụ, nếu một học sinh lớp 11 có chiều cao 148 cm, chúng ta có thể ước tính chiều dài cánh tay của họ khoảng 84 cm.
Kết luận
Trong biểu đồ phân tán này, chúng ta đã khám phá những nền tảng của biểu đồ phân tán và vai trò thiết yếu của chúng trong trực quan hóa và phân tích dữ liệu. Biểu đồ phân tán cung cấp một công cụ mạnh mẽ để minh họa mối quan hệ giữa các biến và phát hiện các mẫu trong dữ liệu. Hãy cùng tóm tắt một số điểm chính từ hướng dẫn này:
- Định nghĩa biểu đồ phân tán:Biểu đồ phân tán, còn được gọi là biểu đồ phân tán hoặc đồ thị phân tán, hiển thị các điểm dữ liệu trên một mặt phẳng hai chiều, mỗi điểm đại diện cho một quan sát duy nhất hoặc một cặp dữ liệu.
- Các biến và trục:Biểu đồ phân tán thường bao gồm hai trục: trục X và trục Y. Hai trục này đại diện cho các biến đang được nghiên cứu, giúp chúng ta hình dung được mối quan hệ giữa sự thay đổi của một biến với sự thay đổi của biến kia.
- Các mẫu tương quan:Biểu đồ phân tán giúp chúng ta nhận diện các mẫu tương quan khác nhau giữa các biến. Các mẫu này có thể được phân loại thành tương quan dương mạnh, tương quan âm mạnh, tương quan dương yếu, tương quan âm yếu, tương quan phức tạp hoặc không có tương quan.
- Các ví dụ thực tế:Trong suốt hướng dẫn, chúng tôi đã cung cấp các ví dụ thực tế để minh họa từng mẫu tương quan này. Từ việc nghiên cứu chiều cao và chiều dài cánh tay học sinh đến phân tích mối quan hệ giữa số giờ học và điểm thi, chúng tôi đã thấy cách biểu đồ phân tán có thể được áp dụng trong nhiều lĩnh vực khác nhau.
- Năng lực dự đoán:Biểu đồ phân tán cho phép chúng ta đưa ra dự đoán về một biến dựa trên biến kia, cung cấp những thông tin quý giá cho việc ra quyết định và hiểu rõ mối quan hệ nhân quả.
- Dữ liệu phức tạp:Biểu đồ phân tán là công cụ linh hoạt có thể xử lý dữ liệu phức tạp, kể cả những tình huống mà mối quan hệ giữa các biến không rõ ràng.
- Giải thích dữ liệu:Khả năng giải thích biểu đồ phân tán là điều thiết yếu đối với các nhà nghiên cứu, chuyên gia phân tích và bất kỳ ai muốn rút ra kết luận có ý nghĩa từ dữ liệu.
- Ứng dụng thực tiễn:Biểu đồ phân tán được ứng dụng trong nhiều lĩnh vực đa dạng như kinh tế, khoa học xã hội, khoa học tự nhiên, kỹ thuật và nhiều lĩnh vực khác. Chúng giúp xác định xu hướng, mối tương quan và các điểm ngoại lệ trong bộ dữ liệu.
Bằng cách thành thạo nghệ thuật tạo ra, phân tích và giải thích biểu đồ phân tán, bạn trang bị cho bản thân một kỹ năng quý giá cho việc ra quyết định dựa trên dữ liệu. Dù bạn là học sinh, nhà nghiên cứu hay chuyên gia, biểu đồ phân tán là một công cụ quý giá trong bộ công cụ phân tích dữ liệu của bạn, mang lại những thông tin giúp thúc đẩy các quyết định sáng suốt và hiểu sâu sắc hơn trong lĩnh vực bạn theo đuổi.

















