Hướng dẫn cho người mới bắt đầu về sơ đồ tham số SysML
Giới thiệu
SysML (Ngôn ngữ mô hình hóa hệ thống) là một công cụ mạnh mẽ để thiết kế các hệ thống phức tạp, và sơ đồ tham số là một thành phần quý giá của SysML giúp mô hình hóa và phân tích các mối quan hệ toán học bên trong một hệ thống. Trong hướng dẫn dành cho người mới bắt đầu này, chúng ta sẽ khám phá những nền tảng của sơ đồ tham số, ý nghĩa của chúng và cách tạo chúng bằng các công cụ mô hình hóa trực quan như Visual Paradigm Online, cung cấp một bộ sưu tập mẫu để đơn giản hóa quá trình.
Sơ đồ tham số là gì?
Sơ đồ tham số trong SysML là các biểu diễn đồ họa được sử dụng để minh họa các mối quan hệ toán học, ràng buộc và phương trình giữa các thành phần hoặc yếu tố khác nhau trong một hệ thống. Những sơ đồ này đặc biệt hữu ích trong việc mô hình hóa và phân tích các ràng buộc hiệu suất và phụ thuộc trong một hệ thống.
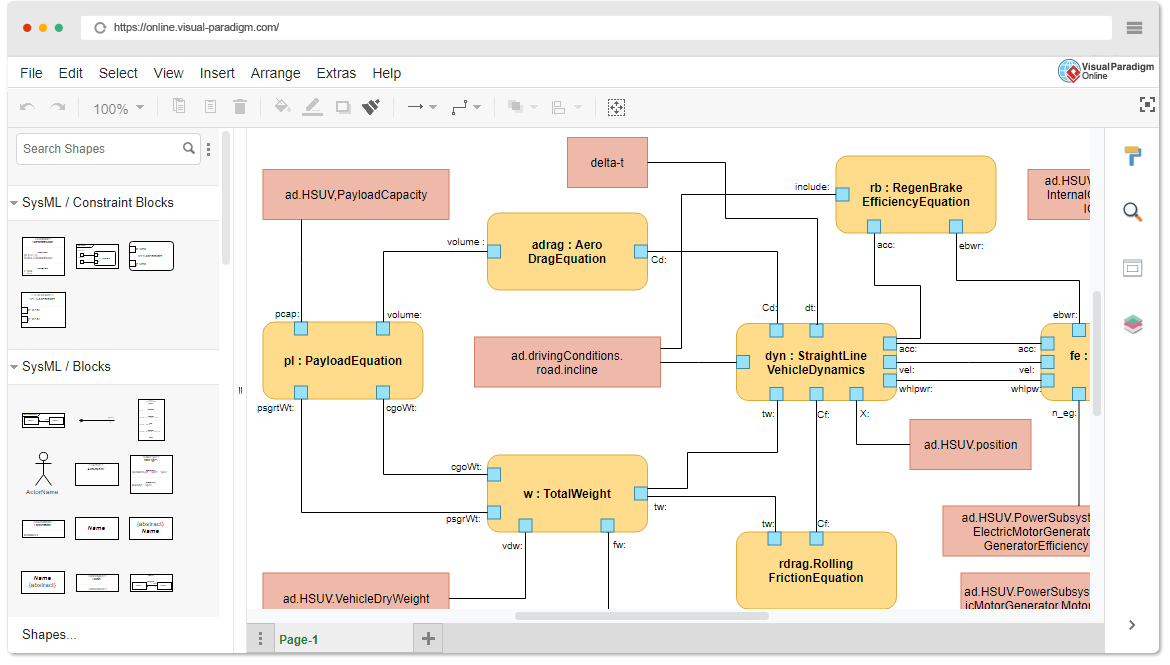
Yêu cầu tiên quyết
Trước khi bắt đầu làm việc với sơ đồ tham số, hãy đảm bảo rằng bạn đang sử dụng profile SysML cho dự án của mình, vì sơ đồ tham số chỉ áp dụng cho profile này.
Các ứng dụng chung của sơ đồ tham số
Sơ đồ tham số phục vụ nhiều mục đích quan trọng trong thiết kế hệ thống:
- Phân tích khách quan các chức năng: Chúng giúp xác định và trực quan hóa các mối quan hệ giữa các chức năng hoặc thành phần khác nhau trong một hệ thống, cho phép phân tích toàn diện.
- Đo lường hiệu quả: Sơ đồ tham số cho phép bạn đo lường hiệu quả của các thành phần hệ thống khác nhau bằng cách mô hình hóa các mối phụ thuộc và ràng buộc của chúng một cách toán học.
- Làm rõ các mối quan hệ: Chúng cung cấp một biểu diễn trực quan rõ ràng về cách một biến hoặc tham số liên quan đến biến hoặc tham số khác, giúp dễ hiểu hơn các hành vi phức tạp của hệ thống.
Tạo sơ đồ tham số
Sơ đồ tham số không phải là các thực thể độc lập; chúng được tạo ra bằng các yếu tố mô hình được gọi làkhối ràng buộc. Những khối này xác định các công thức toán học tổng quát hoặc cơ bản mô tả mối quan hệ giữa các thành phần hệ thống. Dưới đây là hướng dẫn từng bước để tạo sơ đồ tham số:
1. Xác định các khối ràng buộc
Các khối ràng buộc là các khối xây dựng thiết yếu cho sơ đồ tham số. Chúng bao gồm các phương trình và mối quan hệ toán học. Để tạo các khối ràng buộc:
- Truy cập công cụ mô hình hóa của bạn (ví dụ: Visual Paradigm Online).
- Đi đến dự án của bạn và chọn profile SysML.
- Trong một sơ đồ định nghĩa khối, tạo các khối ràng buộc đại diện cho các công thức toán học liên quan đến hệ thống của bạn.
2. Tạo một sơ đồ tham số
Sau khi đã xác định các khối ràng buộc cần thiết, bạn có thể tiếp tục tạo một sơ đồ tham số:
- Trong dự án của bạn, đi đến menu tạo sơ đồ.
- Chọn “Sơ đồ tham số” từ các loại sơ đồ có sẵn.
- Bắt đầu thêm các thuộc tính ràng buộc và kết nối chúng với các khối ràng buộc phù hợp, tạo ra các mối quan hệ toán học trong hệ thống của bạn.
3. Thêm các tham số đầu vào
Trong một sơ đồ tham số, bạn thường cần xác định các tham số đầu vào hoặc giá trị được đưa vào các phương trình được biểu diễn bởi các khối ràng buộc. Những đầu vào này sẽ giúp bạn thực hiện các phép tính và phân tích hành vi của hệ thống dưới các điều kiện khác nhau.
4. Mô hình hóa các mối quan hệ toán học
Kết nối các thuộc tính ràng buộc, các khối ràng buộc và các tham số đầu vào để biểu diễn chính xác các mối quan hệ toán học. Sử dụng các kết nối và chú thích để ghi chép rõ ràng các phương trình và ràng buộc của bạn.
Học qua các ví dụ với Visual Paradigm Online
Visual Paradigm Online cung cấp một số mẫu có thể hỗ trợ bạn trong việc tạo ra Sơ đồ tham số. Bạn có thể bắt đầu bằng cách khám phá các mẫu này và điều chỉnh chúng để phù hợp với nhu cầu thiết kế hệ thống cụ thể của mình. Học qua các ví dụ là một cách hiệu quả để nắm vững các khái niệm và kỹ thuật của sơ đồ tham số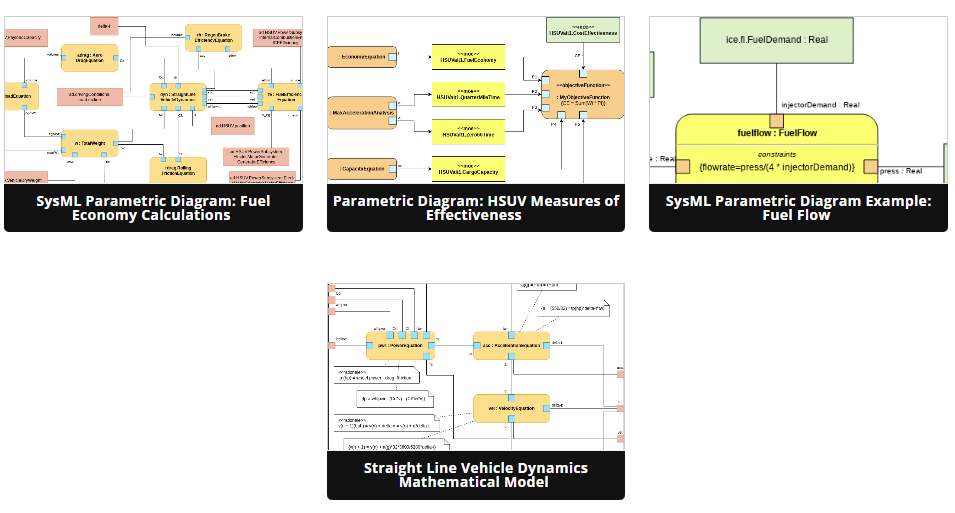
Kết luận
Sơ đồ tham số SysML là công cụ vô giá để mô hình hóa và phân tích các mối quan hệ toán học trong các hệ thống phức tạp. Bằng cách tuân theo các bước được nêu trong hướng dẫn này và sử dụng các công cụ mô hình hóa trực quan như Visual Paradigm Online, bạn có thể thiết kế và phân tích hệ thống một cách hiệu quả, tự tin và chính xác.

















